
分析 将(x2-mx+$\frac{49}{25}$)利用完全平方公式进行配方,然后对应常数相等即可得到m、n的值,所以代入求值即可.
解答 解:x2-mx+$\frac{49}{25}$=(x±$\frac{7}{5}$)2,
则m=-$\frac{14}{5}$,n=$\frac{7}{5}$或m=$\frac{14}{5}$,n=-$\frac{7}{5}$.
所以m+n=-$\frac{14}{5}$+$\frac{7}{5}$=-$\frac{7}{5}$或m+n=$\frac{14}{5}$-$\frac{7}{5}$=$\frac{7}{5}$.
综上所述m+n=±$\frac{7}{5}$.
故答案是:±$\frac{7}{5}$.
点评 本题考查了配方法的应用.二次三项式是完全平方式,则常数项是一次项系数一半的平方.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
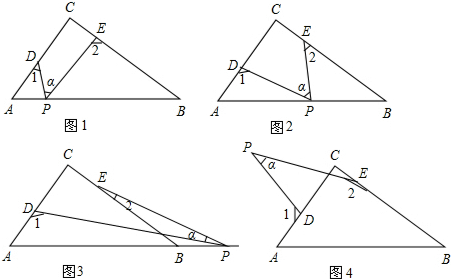
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
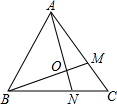 在等边△ABC中,M是AC上一点,N是BC上的一点,且AM=BN,∠MBC=25°,AN与BM交于点O,则∠MON的度数为( )
在等边△ABC中,M是AC上一点,N是BC上的一点,且AM=BN,∠MBC=25°,AN与BM交于点O,则∠MON的度数为( )| A. | 110° | B. | 105° | C. | 90° | D. | 85° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{(-9)(-4)}=\sqrt{-9}•\sqrt{-4}=(-3)(-2)=6$ | B. | $\sqrt{8}-\sqrt{2}=\sqrt{2}$ | ||
| C. | $\sqrt{{3^2}+{4^2}}=3+4=7$ | D. | $\frac{{6-\sqrt{2}}}{{\sqrt{2}}}=3\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com