

���� ��1���ֱ����Բ����СԲ���������������˵÷ֵĸ��ʣ��Ƚϸ��ʼ�����⣻
��2�����������Ͷʯ�ӣ��ֱ�ȷ�����ڲ�ͬ����Ĵ�����Ȼ�������ڲ�����ͼ������Ĵ��������ܴ����������������������
��� �⣺��1��Բ�������Ϊ��32��-22��=5�У�
СԲ�����Ϊ��4�У�
����PС��ʤ=$\frac{5��}{9��}$=$\frac{5}{9}$��
PС��ʤ=$\frac{4��}{9��}$=$\frac{4}{9}$��
������Ϸ����ƽ��
��2�������۾���һ�������������Ͷ��Сʯ�ӣ����ھ�����m�������ࣩܶ�Σ�������ͼ����n�Σ�����ͼ�ε����Ϊ$\frac{n}{m}$��2��3=$\frac{6n}{m}$ƽ���ף�
���� ���⿼��������Ƶ�ʹ��Ƹ��ʼ���Ϸ��ƽ�Ե�֪ʶ������Ĺؼ����ܹ�ȷ�����ʣ��ѶȲ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
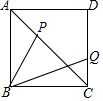 ��ͼ��������ABCD�У���֪AB=2������P��Q�ֱ���AC��CD�ϣ���AP=CQ����BP+BQ��2����Сֵ��8+4$\sqrt{2}$��
��ͼ��������ABCD�У���֪AB=2������P��Q�ֱ���AC��CD�ϣ���AP=CQ����BP+BQ��2����Сֵ��8+4$\sqrt{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
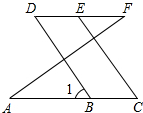 �����������˵����
�����������˵�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
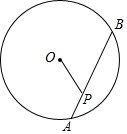 ��ͼ��ԲO��ֱ��Ϊ10cm����AB�ij�Ϊ8cm��P����AB��һ�㣬��OP�ij��������������������ĵ�P�м�����������
��ͼ��ԲO��ֱ��Ϊ10cm����AB�ij�Ϊ8cm��P����AB��һ�㣬��OP�ij��������������������ĵ�P�м�����������| A�� | 8 | B�� | 7 | C�� | 6 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �� | B�� | �� | C�� | �� | D�� | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com