
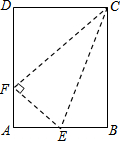
 如图,已知矩形ABCD的两边AB与BC的比为4:5,E是AB上的一点,沿CE将△EBC向上翻折,若B点恰好落在边AD上的F点,则tan∠DCF=$\frac{3}{4}$.
如图,已知矩形ABCD的两边AB与BC的比为4:5,E是AB上的一点,沿CE将△EBC向上翻折,若B点恰好落在边AD上的F点,则tan∠DCF=$\frac{3}{4}$.  课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:选择题
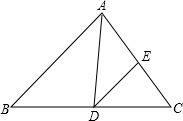 如图,在△ABC中,∠B=46°,∠ADE=40°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠C的大小是( )
如图,在△ABC中,∠B=46°,∠ADE=40°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠C的大小是( )| A. | 46° | B. | 66° | C. | 54° | D. | 80° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
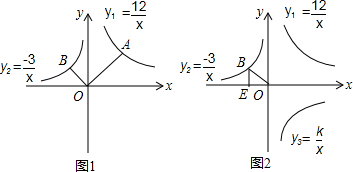
| A. | 1 | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
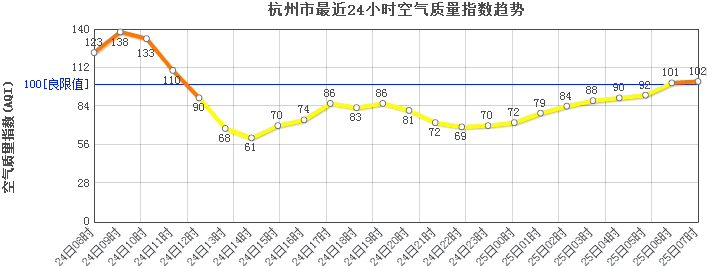
| A. | 在这个24小时中,AQI的值超过良限值时段是24日08时至24日12时 | |
| B. | 在这个24小时中,AQI对应的颜色为黄色的时段持续了20小时以上 | |
| C. | 在这个24小时中,AQI的最大值和最小值的差为77 | |
| D. | 建议中老年朋友在25日06时至07时进行晨练 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
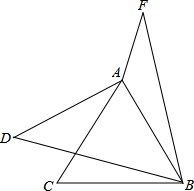 如图,已知等边△ABC,点D在AC的外侧,将BD绕点B顺时针旋转60°至BF,点F与点D相对应,连接AF,AD,AD=2,∠CBD=15°,∠AFB=30°,则AF的长为$\sqrt{6}-\sqrt{2}$.
如图,已知等边△ABC,点D在AC的外侧,将BD绕点B顺时针旋转60°至BF,点F与点D相对应,连接AF,AD,AD=2,∠CBD=15°,∠AFB=30°,则AF的长为$\sqrt{6}-\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com