
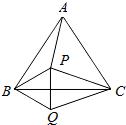
 如图所示,点P是等边三角形ABC内的一点,连接PA、PB、PC以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
如图所示,点P是等边三角形ABC内的一点,连接PA、PB、PC以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
|


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
 如图,A、B两点的坐标分别是(1,
如图,A、B两点的坐标分别是(1,| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、86;87 |
| B、87;86 |
| C、86.5;87 |
| D、87;86.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 先作图,再证明.
先作图,再证明.查看答案和解析>>
科目:初中数学 来源: 题型:
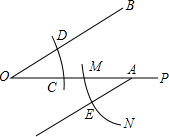 已知∠BOP与OP上点C,点A(在点C的右边),李玲现进行如下操作:①以点O为圆心,OC长为半径画弧,交OB于点D,连接CD;②以点A为圆心,OC长为半径画弧MN,交OA于点M;③以点M为圆心,CD长为半径画弧,交弧MN于点E,连接ME,操作结果如图所示,下列结论不能由上述操作结果得出的是( )
已知∠BOP与OP上点C,点A(在点C的右边),李玲现进行如下操作:①以点O为圆心,OC长为半径画弧,交OB于点D,连接CD;②以点A为圆心,OC长为半径画弧MN,交OA于点M;③以点M为圆心,CD长为半径画弧,交弧MN于点E,连接ME,操作结果如图所示,下列结论不能由上述操作结果得出的是( )| A、CD∥ME |
| B、OB∥AE |
| C、∠ODC=∠AEM |
| D、∠ACD=∠EAP |
查看答案和解析>>
科目:初中数学 来源: 题型:
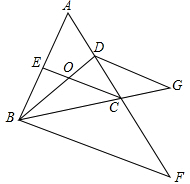 如图,△ABC中,∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,BD,CE交于点O,F,G分别是AC,BC延长线上一点,且∠EOD+∠OBF=180°,∠DBC=∠G,指出图中所有平行线,并说明理由.
如图,△ABC中,∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,BD,CE交于点O,F,G分别是AC,BC延长线上一点,且∠EOD+∠OBF=180°,∠DBC=∠G,指出图中所有平行线,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
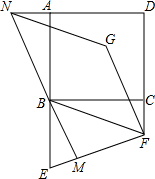 如图,已知正方形ABCD,E是AB延长线上一点,F是DC延长线上一点,连接BF、EF,恰有BF=EF,将线段EF绕点F顺时针旋转90°得FG,过点B作EF的垂线,交EF于点M,交DA的延长线于点N,连接NG.
如图,已知正方形ABCD,E是AB延长线上一点,F是DC延长线上一点,连接BF、EF,恰有BF=EF,将线段EF绕点F顺时针旋转90°得FG,过点B作EF的垂线,交EF于点M,交DA的延长线于点N,连接NG.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,一扇形纸扇完全打开后,外侧两竹条AB、AC的夹角为120°,AB长为30cm,贴纸部分BD长为20cm,贴纸部分的面积为( )cm2.
如图,一扇形纸扇完全打开后,外侧两竹条AB、AC的夹角为120°,AB长为30cm,贴纸部分BD长为20cm,贴纸部分的面积为( )cm2.A、
| ||
B、
| ||
| C、800π | ||
| D、500π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com