
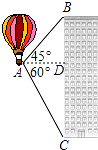
 如图,热气球的探测器在点A,从热气球看一栋高楼的顶部B的仰角为45°,看这栋高楼底部C的俯角为60°,热气球与高楼的水平距离AD为30米,求这栋楼的高度($\sqrt{3}$取1.73,结果精确到0.1米).
如图,热气球的探测器在点A,从热气球看一栋高楼的顶部B的仰角为45°,看这栋高楼底部C的俯角为60°,热气球与高楼的水平距离AD为30米,求这栋楼的高度($\sqrt{3}$取1.73,结果精确到0.1米). 分析 根据垂直的定义得到∠BDA=∠CDA=90°,解直角三角形得到BD=AD•tan∠BAD=30×tan45°=30(米),解直角三角形得到CD=AD•tan∠CAD=30×tan60°=$30\sqrt{3}$≈51.9,即可得到结论.
解答  解:由题意,AD⊥BC于D,即∠BDA=∠CDA=90°,
解:由题意,AD⊥BC于D,即∠BDA=∠CDA=90°,
∵∠BDA=90°,∠BAD=45°,AD=30,
∴BD=AD•tan∠BAD=30×tan45°=30(米),
∵∠CDA=90°,∠CAD=60°,AD=30,
∴CD=AD•tan∠CAD=30×tan60°=$30\sqrt{3}$≈51.9,
∴BC=BD+CD≈81.9(米).
答:这栋楼的高度约为81.9米.
点评 本题考查了解直角三角形的应用--仰角俯角问题,将原三角形转化为两个直角三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 小丽想测量学校旗杆的高度,她在地面A点安置侧倾器,测得旗杆顶端C的仰角为α,侧倾器到旗杆底部的距离AD为10米,侧倾器的高度AB为1.5米,那么旗杆的高度CD为( )
小丽想测量学校旗杆的高度,她在地面A点安置侧倾器,测得旗杆顶端C的仰角为α,侧倾器到旗杆底部的距离AD为10米,侧倾器的高度AB为1.5米,那么旗杆的高度CD为( )| A. | (10tanα+1.5)米 | B. | (10cosα+1.5)米 | C. | ($\frac{10}{tanα}$+1.5)米 | D. | ($\frac{10}{sinα}$+1.5)米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
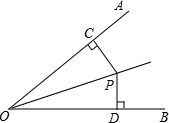 如图,若OP平分∠AOB,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论中错误的是( )
如图,若OP平分∠AOB,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论中错误的是( )| A. | PC=PD | B. | OC=PC | C. | ∠CPO=∠DPO | D. | OC=OD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com