练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．解方程
    （1）x2-2x-1=0                 
    （2）（x-3）2-2x（3-x）=0．

    分析 （1）利用配方法求得方程的解即可；
    （2）利用因式分解法解方程即可．

    解答 解：（1）x2-2x-1=0
    x2-2x=1
    x2-2x+1=2
    （x-1）2=2
    x-1=±$\sqrt{2}$
    解得：x1=1+$\sqrt{2}$，x2=1-$\sqrt{2}$；

    （2）（x-3）2-2x（3-x）=0
    （x-3）（x-3+2x）=0
    x-3=0，3x-3=0，
    解得：x1=3，x2=1．

    点评 本题考查了利用配方法和因式分解法解一元二次方程，解此题的关键是能根据方程的特点选择适当的方法解一元二次方程．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    20．计算与化筒：
    （1）8x2•（-$\frac{3x}{4{y}^{3}}$）•（-$\frac{6z}{{x}^{2}y}$）
    （2）$\frac{3{b}^{2}}{16a}$÷$\frac{bc}{2{a}^{2}}$•（-$\frac{2a}{b}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

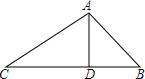    7．先阅读材料．再解答下面的问题：问题：在△ABC中，AD是边BC上的高，AD=2，DB=2，CD=2$\sqrt{3}$，求∠BAC的度数．
    王刚是这样解答的：
    如图．在Rt△ACD中，tan∠CAD=$\frac{CD}{AD}$=$\sqrt{3}$，则∠CAD=60°．在Rt△ADB中，tan∠BAD=$\frac{BD}{AD}$=1，则∠BAD=45°．
    ∴∠BAC=∠CAD+∠BAD=105°．你认为王刚的解法正确吗？为什么？如果不正确．请指出错误之处．并写出正确的答案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．读出下列语句，并按照这些语句分别画出图形．
    （1）直线a和直线AB相交于点P；
    （2）直线1经过点A、B，点C在线段AB上；
    （3）直线a经过点A、B，点P不在直线a上．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

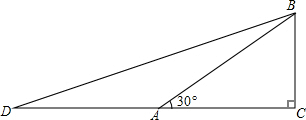    11．若想求cos15°的值，可先画Rt△ABC，使∠C=90°，∠BAC=30°，再延长CA到D，使DA=AB，连结BD．利用这些条件，你能否求出tan15°的值？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

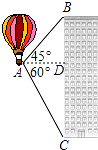    1．如图，热气球的探测器在点A，从热气球看一栋高楼的顶部B的仰角为45°，看这栋高楼底部C的俯角为60°，热气球与高楼的水平距离AD为30米，求这栋楼的高度（$\sqrt{3}$取1.73，结果精确到0.1米）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．已知点A（a，-1）与点B（5，b）关于原点对称，则ab的值为-5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

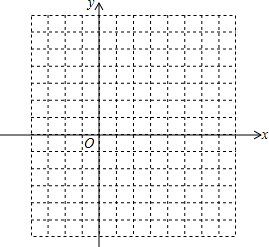    5．已知二次函数y=x2-2x-3．
    （1）将y=x2-2x-3化成y=a（x-h）2+k的形式；
    （2）与y轴的交点坐标是（0，-3），与x轴的交点坐标是（3，0）（-1，0）；
    （3）在坐标系中利用描点法画出此抛物线．
    x……
    y……
    （4）不等式x2-2x-3＞0的解集是x＜-1或x＞3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．计算：（3x）-3÷（x-2y-1）=$\frac{y}{27x}$．

    查看答案和解析>>

    同步练习册答案