
【题目】如图,平面直角坐标系中有一正方形OABC,点C的坐标为(﹣2,﹣1),则点A坐标为_____,点B坐标为_____.
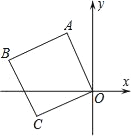
【答案】 (﹣1,2) (﹣3,1)
【解析】分析:过点A作AD⊥y轴于D,过点C作CE⊥x轴,过点B作BF⊥CE交CE的延长线于F,根据点C的坐标求出![]() ,再根据正方形的性质可得
,再根据正方形的性质可得![]() ,再求出∠AOD=∠COE=∠BCF,然后求出△AOD≌△COE≌△BCF,根据全等三角形对应边相等可得AD=CE=BF=1,OD=OE=CF=2,然后求解即可.
,再求出∠AOD=∠COE=∠BCF,然后求出△AOD≌△COE≌△BCF,根据全等三角形对应边相等可得AD=CE=BF=1,OD=OE=CF=2,然后求解即可.
详解:如图,过点A作AD⊥y轴于D,过点C作CE⊥x轴,过点B作BF⊥CE交CE的延长线于F,
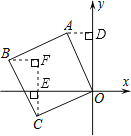
∵C(2,1),
∴OE=2,CE=1,
∵四边形OABC是正方形,
∴OA=OC=BC,
易求∠AOD=∠COE=∠BCF,
又∵![]()
∴△AOD≌△COE≌△BCF,
∴AD=CE=BF=1,OD=OE=CF=2,
∴点A的坐标为(1,2),EF=21=1,
点B到y轴的距离为1+2=3,
∴点B的坐标为(3,1).
故答案为:(1,2);(3,1).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,以O为圆心的弧BD度数为60°,∠BOE=45°,DA⊥OB,EB⊥OB.
(1)求![]() 的值;
的值;
(2)若OE与弧BD交于点M,OC平分∠BOE,连接CM.说明CM为⊙O的切线;(3)在(2)的条件下,若BC=1,求tan∠BCO的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】读题画图计算并作答
画线段AB=3 cm,在线段AB上取一点K,使AK=BK,在线段AB的延长线上取一点C,使AC=3BC,在线段BA的延长线取一点D,使AD=![]() AB.
AB.
(1)求线段BC、DC的长?
(2)点K是哪些线段的中点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】骰子是6个面上分别写有数字1,2,3,4,5,6的小立方体,它任意两对面上所写的两个数字之和为7.将这样相同的几个骰子按照相接触的两个面上的数字的积为6摆成一个几何体,这个几何体的三视图如图所示.已知图中所标注的是部分面上的数字,则“*”所代表的数是( )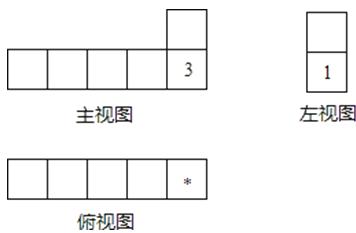
A.2
B.4
C.5
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
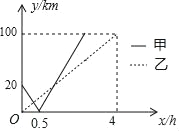
【题目】沿河岸有A,B,C三个港口,甲乙两船同时分别从AB港口出发,匀速驶向C港,最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.考察下列结论:
①乙船的速度是25km/h;②从A港到C港全程为120km;③甲船比乙船早1.5小时到达终点;④若设图中两者相遇的交点为P点,P点的坐标为(![]() ,
,![]() );⑤如果两船相距小于10km能够相互望见,那么甲、乙两船可以相互望见时,x的取值范围是
);⑤如果两船相距小于10km能够相互望见,那么甲、乙两船可以相互望见时,x的取值范围是![]() <x<2.其中正确的结论有_____.
<x<2.其中正确的结论有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,地震、泥石流等自然灾害频繁发生,造成极大的生命和财产损失.为了更好地做好“防震减灾”工作,我市相关部门对某中学学生“防震减灾”的知晓率采取随机抽样的方法进行问卷调查,调查结果分为“非常了解”、“比较了解”、“基本了解”和“不了解”四个等级.小明根据调查结果绘制了如下统计图,请根据提供的信息回答问题: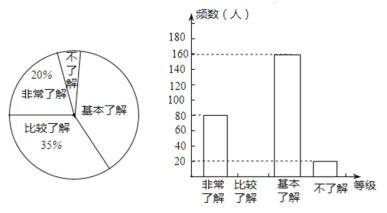
(1)本次参与问卷调查的学生有多少人;扇形统计图中“基本了解”部分所对应的扇形圆心角是多少度;在该校2000名学生中随机提问一名学生,对“防震减灾”不了解的概率为多少.
(2)请补全频数分布直方图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蜗牛从某点![]() 开始沿一东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米):
开始沿一东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 通过计算说明蜗牛是否回到起点
通过计算说明蜗牛是否回到起点![]() .
.
![]() 蜗牛离开出发点
蜗牛离开出发点![]() 最远时是多少厘米?
最远时是多少厘米?
![]() 在爬行过程中,如果每爬
在爬行过程中,如果每爬![]() 厘米奖励
厘米奖励![]() 粒芝麻,则蜗牛一共得到多少粒芝麻?
粒芝麻,则蜗牛一共得到多少粒芝麻?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com