
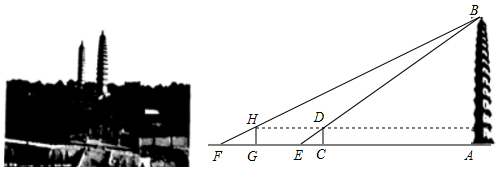
分析 易知△EDC∽△EBA,△FHC∽△FBA,可得$\frac{GH}{BA}$=$\frac{FG}{FA}$,$\frac{DC}{BA}$=$\frac{EC}{EA}$,因为DC=HG,推出$\frac{FG}{FA}$=$\frac{EC}{EA}$,列出方程求出CA=106(米),由$\frac{DC}{BA}$=$\frac{EC}{EA}$,可得$\frac{2}{BA}$=$\frac{4}{4+106}$,由此即可解决问题.
解答 解:∵△EDC∽△EBA,△FHC∽△FBA,
∴$\frac{GH}{BA}$=$\frac{FG}{FA}$,$\frac{DC}{BA}$=$\frac{EC}{EA}$,∵DC=HG,
∴$\frac{FG}{FA}$=$\frac{EC}{EA}$,
∴$\frac{6}{59+CA}$=$\frac{4}{4+CA}$,
∴CA=106(米),
∵$\frac{DC}{BA}$=$\frac{EC}{EA}$,
∴$\frac{2}{BA}$=$\frac{4}{4+106}$,
∴AB=55(米),
答:舍利塔的高度AB为55米.
点评 本题考查解直角三角形的应用、相似三角形的判定和性质,解题的关键是灵活运用所学知识解决问题,学会构建方程解决问题,属于中考常考题型.


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 6 | B. | 5 | C. | $12+2\sqrt{13}$ | D. | $12-2\sqrt{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com