
【题目】如图,在平面直角坐标系中,以O为圆心作⊙O交x轴正半轴于A,P为⊙O上的动点(点P不在坐标轴上),过点P作PC⊥x轴,PD⊥y轴于点C、D,B为CD中点,连接AB则∠BAO的最大值是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
连接OP,以O为圆心,以![]() OP为半径作圆,根据矩形的判定证出四边形OCPD为矩形,再根据矩形的性质可得CD=OP,且CD、OP互相平分,再结合已知,从而得出B为OP的中点,即OB=
OP为半径作圆,根据矩形的判定证出四边形OCPD为矩形,再根据矩形的性质可得CD=OP,且CD、OP互相平分,再结合已知,从而得出B为OP的中点,即OB=![]() OP,即可得出以O为圆心,以
OP,即可得出以O为圆心,以![]() OP为半径作圆即为B点的运动轨迹,再根据图形可知:当AB是此圆的切线时,∠BAO最大,根据切线的性质可得∠OBA=90°,根据锐角三角函数即可求出此时∠BAO.
OP为半径作圆即为B点的运动轨迹,再根据图形可知:当AB是此圆的切线时,∠BAO最大,根据切线的性质可得∠OBA=90°,根据锐角三角函数即可求出此时∠BAO.
解:连接OP,以O为圆心,以![]() OP为半径作圆,如图所示
OP为半径作圆,如图所示
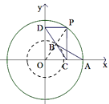
∵PC⊥x轴,PD⊥y轴,x轴⊥y轴
∴四边形OCPD为矩形
∴CD=OP,且CD、OP互相平分
∵B为CD的中点
∴B为OP的中点,即OB=![]() OP
OP
∴以O为圆心,以![]() OP为半径作圆即为B点的运动轨迹
OP为半径作圆即为B点的运动轨迹
由图可知,当AB是此圆的切线时,∠BAO最大
∴此时∠OBA=90°
∴sin∠BAO=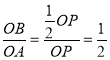
∴∠BAO=30°
故选B.


科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD的边BC延长线上一点,联结DE,过顶点B作BF⊥DE,垂足为F,BF交边DC于点G.
(1)求证:GDAB=DFBG;
(2)联结CF,求证:∠CFB=45°.
查看答案和解析>>
科目:初中数学 来源: 题型:
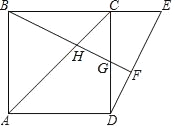
【题目】如图,矩形ABCD中,AB=![]() ,BC=12,E为AD中点,F为AB上一点,将△AEF沿EF折叠后,点A恰好落到CF上的点G处,则折痕EF的长是_______ .
,BC=12,E为AD中点,F为AB上一点,将△AEF沿EF折叠后,点A恰好落到CF上的点G处,则折痕EF的长是_______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(感知)如图①,在四边形![]() 中,点
中,点![]() 在边
在边![]() 上(点
上(点![]() 不与点
不与点![]() 、
、![]() 重合),
重合),![]() .易证:
.易证:![]() (不要求证明).
(不要求证明).
(探究)如图②,在四边形![]() 中,点
中,点![]() 在边
在边![]() 上(点
上(点![]() 不与点
不与点![]() 、
、![]() 重合),
重合),![]() .
.
(1)求证:![]() .
.
(2)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
(应用)如图③,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上(点
上(点![]() 不与点
不与点![]() 、
、![]() 重合),连结
重合),连结![]() ,作
,作![]() ,
,![]() 与边
与边![]() 交于点
交于点![]() .当
.当![]() 时,求
时,求![]() 的长.
的长.
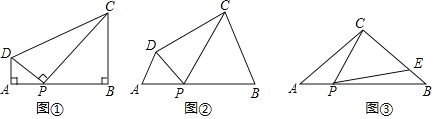
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展校园“美德少年”评选活动,共有“助人为乐”,“自强自立”、“孝老爱亲”,“诚实守信”四种类别,每位同学只能参评其中一类,评选后,把最终入选的20位校园“美德少年”分类统计,制作了如下统计表,后来发现,统计表中前两行的数据都是正确的,后两行的数据中有一个是错误的.
类别 | 频数 | 频率 |
助人为乐美德少年 | a | 0.20 |
自强自立美德少年 | 3 | b |
孝老爱亲美德少年 | 7 | 0.35 |
诚实守信美德少年 | 6 | 0.32 |
根据以上信息,解答下列问题:
(1)统计表中的a= ,b ;
(2)统计表后两行错误的数据是 ,该数据的正确值是 ;
(3)校园小记者决定从A,B,C三位“自强自立美德少年”中随机采访两位,用画树状图或列表的方法,求A,B都被采访到的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面上两点A,B,给出如下定义:以点A或B为圆心,AB长为半径的圆称为点A,B的“确定圆”.如图为点A,B的“确定圆”的示意图.
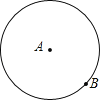
(1)已知点A的坐标为(-1,0),点B的坐标为(3,3),则点A,B的“确定圆”的面积为______;
(2)已知点A的坐标为(0,0),若直线y=x+b上只存在一个点B,使得点A,B的“确定圆”的面积为9π,求点B的坐标;
(3)已知点A在以P(m,0)为圆心,以1为半径的圆上,点B在直线![]() 上,若要使所有点A,B的“确定圆”的面积都不小于9π,直接写出m的取值范围.
上,若要使所有点A,B的“确定圆”的面积都不小于9π,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
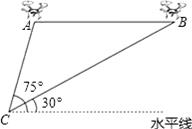
【题目】某兴趣小组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是正三角形ABC内一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后得到△P'AB.给出下列四个结论:①PP'=6,②AP2+BP2=CP2,③∠APB=150°;④S△ABC=36+25![]() .正确结论个数为( )
.正确结论个数为( )

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场去年种植了10亩地的南瓜,亩产量为2000![]() ,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,已知南瓜种植面积的增长率是亩产量的增长率的2倍,今年南瓜的总产量为60 000kg,求南瓜亩产量的增长率.
,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,已知南瓜种植面积的增长率是亩产量的增长率的2倍,今年南瓜的总产量为60 000kg,求南瓜亩产量的增长率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com