
【题目】如图,P是正三角形ABC内一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后得到△P'AB.给出下列四个结论:①PP'=6,②AP2+BP2=CP2,③∠APB=150°;④S△ABC=36+25![]() .正确结论个数为( )
.正确结论个数为( )

A.1B.2C.3D.4
【答案】D
【解析】
由已知△PAC绕点A逆时针旋转后,得到△P′AB,可得△PAC≌△P′AB,PA=P′A,旋转角∠P′AP=∠BAC=60°,所以△APP′为等边三角形,即可求得PP′,由勾股定理逆定理可求△PP'B是直角三角形,AP2+BP2=CP2,可得∠P'PB=90°,可得∠APB=150°,过点A作AD垂直BP于点D,算出AD、PD,再用勾股定理算出AB,然后用公式直接求出面积.
解:连接PP′,过点A作AD⊥BP于点D,如图,
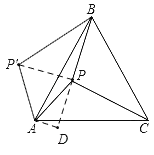
由旋转性质可知,△APC≌△AP'B,
∴AP=AP',P'B=PC=10,
∵∠P'AP=60°,
∴△APP'是等边三角形,
∴PP'=AP=6,故①正确;
∵PB=8,
∴P'B2=PB2+P'P2,
∴△PP'B是直角三角形,AP2+BP2=CP2,故②正确
∴∠P'PB=90°,
∵∠P'PA=60°,
∴∠APB=150°,故③正确;
∴∠APD=30°,
∴AD=![]() AP=3,PD=3
AP=3,PD=3![]() ,
,
∴BD=8+3![]() ,
,
在Rt△ABD中,AB2=AD2+BD2=100+48![]() ,
,
∴S△ABC=![]() AB2=36+25
AB2=36+25![]() ,故④正确.
,故④正确.
故选:D.


科目:初中数学 来源: 题型:
【题目】密闭容器内有一定质量的二氧化碳,当容器的体积V(单位:m3)变化时,气体的密度ρ(单位:kg/m3)随之变化,已知密度ρ与体积V是反比例函数关系,它的图象如图所示.
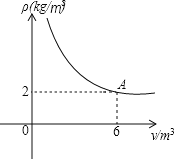
(1)求密度ρ关于体积V的函数解析式;
(2)当密度ρ不低于4kg/m3时,求二氧化碳体积的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以O为圆心作⊙O交x轴正半轴于A,P为⊙O上的动点(点P不在坐标轴上),过点P作PC⊥x轴,PD⊥y轴于点C、D,B为CD中点,连接AB则∠BAO的最大值是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
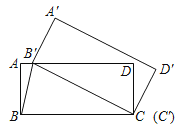
【题目】如图,把某矩形纸片ABCD沿EF、GH折叠(点E、H在AD边上,点F、G在BC边上),使得点B、点C落在AD边上同一点P处,A点的对称点为![]() 点,D点的对称点为
点,D点的对称点为![]() 点,若
点,若![]() ,
,![]() 的面积为4,
的面积为4,![]() 的面积为1,则矩形ABCD的面积等于_____.
的面积为1,则矩形ABCD的面积等于_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,BC=4,将矩形ABCD绕点C顺时针旋转得到矩形A′B′C′D'.设旋转角为α,此时点B′恰好落在边AD上,连接B'B.
(1)当B'恰好是AD中点时,此时α= ;
(2)若∠AB'B=75°,求旋转角α及AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
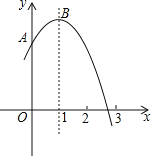
【题目】如图,抛物线![]() (m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.①抛物线
(m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.①抛物线![]() 与直线
与直线![]() 有且只有一个交点;②若点
有且只有一个交点;②若点![]() 、点
、点![]() 、点
、点![]() 在该函数图象上,则
在该函数图象上,则![]() ;③将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为
;③将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为![]() ;④点A关于直线
;④点A关于直线![]() 的对称点为C,点D、E分别在x轴和y轴上,当
的对称点为C,点D、E分别在x轴和y轴上,当![]() 时,四边形BCDE周长的最小值为
时,四边形BCDE周长的最小值为![]() .其中正确判断的序号是__
.其中正确判断的序号是__
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,sin∠AOB=,反比例函数y=(k>0)在第一象限内的图象经过点A,与BC交于点F.

(1)若OA=10,求反比例函数解析式;
(2)若点F为BC的中点,且△AOF的面积S=12,求OA的长和点C的坐标;
(3)在(2)中的条件下,过点F作EF∥OB,交OA于点E(如图②),点P为直线EF上的一个动点,连接PA,PO.是否存在这样的点P,使以P、O、A为顶点的三角形是直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (
(![]() 、
、![]() 、
、![]() 为常数,
为常数,![]() )经过点
)经过点![]() ,
,![]() ,
,![]() .
.
(1)求抛物线的解析式;
(2)如图,在直线![]() 下方的抛物线上是否存在点
下方的抛物线上是否存在点![]() 使四边形
使四边形![]() 的面积最大?若存在,请求出点
的面积最大?若存在,请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
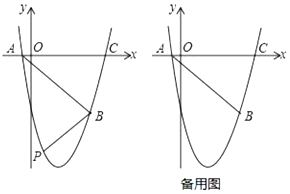
(3)若点![]() 为抛物线的对称轴上的一个动点,试指出
为抛物线的对称轴上的一个动点,试指出![]() 为等腰三角形的点
为等腰三角形的点![]() 共有几个?并求以
共有几个?并求以![]() 为底边时,点
为底边时,点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘潜艇在海面下500米A处测得俯角为30°的海底C处有一黑匣子发出信号,继续在同一深度直线航行4000米后,在B处测得俯角为60°的海底也有该黑匣子发出的信号,则黑匣子所在位置点C在海面下的深度为( )
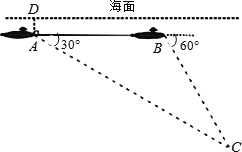
A. 2000米 B. 4000米 C. 2000米 D. (2000![]() +500)米
+500)米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com