
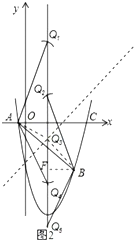
【题目】如图,抛物线![]() (
(![]() 、
、![]() 、
、![]() 为常数,
为常数,![]() )经过点
)经过点![]() ,
,![]() ,
,![]() .
.
(1)求抛物线的解析式;
(2)如图,在直线![]() 下方的抛物线上是否存在点
下方的抛物线上是否存在点![]() 使四边形
使四边形![]() 的面积最大?若存在,请求出点
的面积最大?若存在,请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
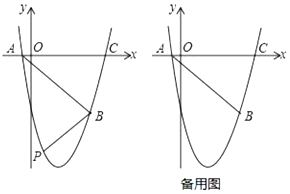
(3)若点![]() 为抛物线的对称轴上的一个动点,试指出
为抛物线的对称轴上的一个动点,试指出![]() 为等腰三角形的点
为等腰三角形的点![]() 共有几个?并求以
共有几个?并求以![]() 为底边时,点
为底边时,点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() ;(3)点
;(3)点![]() 的坐标为:
的坐标为: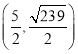 或
或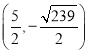 或
或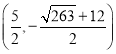 或
或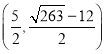 或
或![]() .
.
【解析】
(1)抛物线经过点![]() ,
,![]() ,
,![]() ,可利用两点式法设抛物线的解析式为
,可利用两点式法设抛物线的解析式为![]() ,代入
,代入![]() 即可求得函数的解析式;
即可求得函数的解析式;
(2)作辅助线,将四边形![]() 分成三个图形,两个三角形和一个梯形,设
分成三个图形,两个三角形和一个梯形,设![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,用字母
,用字母![]() 表示出四边形
表示出四边形![]() 的面积
的面积![]() ,发现是一个二次函数,利用顶点坐标求极值,从而求出点
,发现是一个二次函数,利用顶点坐标求极值,从而求出点![]() 的坐标.
的坐标.
(3)分三种情况画图:①以![]() 为圆心,
为圆心,![]() 为半径画弧,交对称轴于
为半径画弧,交对称轴于![]() 和
和![]() ,有两个符合条件的
,有两个符合条件的![]() 和
和![]() ;②以
;②以![]() 为圆心,以
为圆心,以![]() 为半径画弧,也有两个符合条件的
为半径画弧,也有两个符合条件的![]() 和
和![]() ;③作
;③作![]() 的垂直平分线交对称轴于一点
的垂直平分线交对称轴于一点![]() ,有一个符合条件的
,有一个符合条件的![]() ;最后利用等腰三角形的腰相等,利用勾股定理列方程求出
;最后利用等腰三角形的腰相等,利用勾股定理列方程求出![]() 坐标.
坐标.
解:(1)设![]() ,
,
把![]() 代入:
代入:![]() ,
,
![]() ,
,
∴![]() ;
;
(2)存在,
如图1,分别过![]() 、
、![]() 向
向![]() 轴作垂线
轴作垂线![]() 和
和![]() ,垂足分别为
,垂足分别为![]() 、
、![]() ,
,

设![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
当![]() 时,
时,![]() 有最大值为48,这时
有最大值为48,这时![]() ,
,
∴![]() ,
,
(3)这样的![]() 点一共有5个,
点一共有5个,
①以![]() 为圆心,以
为圆心,以![]() 为半径画弧,交抛物线的对称轴于
为半径画弧,交抛物线的对称轴于![]() 、
、![]() ,则
,则![]() ,
,
设对称轴交![]() 轴于
轴于![]() ,
,
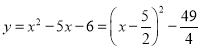 ;
;
∴抛物线的对称轴是:![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
由勾股定理得: ,
,
∴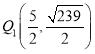 ,
,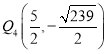
②以![]() 为圆心,以
为圆心,以![]() 为半径画弧,交抛物线的对称轴于
为半径画弧,交抛物线的对称轴于![]() 、
、![]() ,
,
∴![]() ,
,
过![]() 作
作![]() 于
于![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() ,
,
由勾股定理得: ,
,
∴![]() ,
,
∴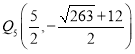 ,
,
∵![]() ,
,
∴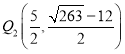 ,
,
③连接![]() 、
、![]() ,
,
因为![]() 在对称轴上,所以设
在对称轴上,所以设![]() ,
,
∵![]() 是等腰三角形,且
是等腰三角形,且![]() ,
,
由勾股定理得: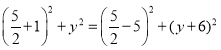 ,
,
![]() ,
,
∴![]() .
.
综上所述,点![]() 的坐标为:
的坐标为: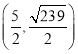 或
或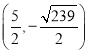 或
或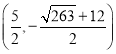 或
或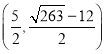 或
或![]() .
.


科目:初中数学 来源: 题型:
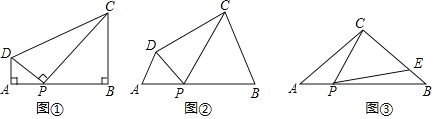
【题目】(感知)如图①,在四边形![]() 中,点
中,点![]() 在边
在边![]() 上(点
上(点![]() 不与点
不与点![]() 、
、![]() 重合),
重合),![]() .易证:
.易证:![]() (不要求证明).
(不要求证明).
(探究)如图②,在四边形![]() 中,点
中,点![]() 在边
在边![]() 上(点
上(点![]() 不与点
不与点![]() 、
、![]() 重合),
重合),![]() .
.
(1)求证:![]() .
.
(2)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
(应用)如图③,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上(点
上(点![]() 不与点
不与点![]() 、
、![]() 重合),连结
重合),连结![]() ,作
,作![]() ,
,![]() 与边
与边![]() 交于点
交于点![]() .当
.当![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是正三角形ABC内一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后得到△P'AB.给出下列四个结论:①PP'=6,②AP2+BP2=CP2,③∠APB=150°;④S△ABC=36+25![]() .正确结论个数为( )
.正确结论个数为( )

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮参加中华诗词大赛,还剩最后两题,如果都答对,就可顺利通关.其中第一道单选题有4个选项,第二道单选题有3个选项.小亮这两道题都不会,不过还有一个“求助”没有使用(使用求助可以让主持人去掉其中一题的一个错误选项).
(1)如果小亮第一题使用“求助”,那么他答对第一道题的概率是__;
(2)他的亲友团建议:最后一题使用“求助”,从提高通关的可能性的角度看,你同意亲友团的观点吗?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一幅长为60 cm,宽为40 cm的矩形风景画的四周镶一条相同宽度的纸边,制成一幅矩形挂图.若要使整个挂图的面积是3 500 cm2,设纸边的宽为x cm,则根据题意可列方程为( )

A. (60+x)(40+x)=3 500 B. (60+2x)(40+2x)=3 500
C. (60-x)(40-x)=3 500 D. (60-2x)(40-2x)=3 500
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场去年种植了10亩地的南瓜,亩产量为2000![]() ,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,已知南瓜种植面积的增长率是亩产量的增长率的2倍,今年南瓜的总产量为60 000kg,求南瓜亩产量的增长率.
,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,已知南瓜种植面积的增长率是亩产量的增长率的2倍,今年南瓜的总产量为60 000kg,求南瓜亩产量的增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从A地到B地的公路需要经过C地,根据规划,将在A,B两地之间修建一条笔直的公路.已知AC=10千米,∠CAB=34°,∠CBA=45°,求改直后公路AB的长(结果精确到0.1千米)
(参考数据:sin34°≈0.559,cos34°≈0.829,tan34°≈0.675)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让同学们了解自己的体育水平,八年级![]() 班的体育老师对全班
班的体育老师对全班![]() 名学生进行了一次体育模拟测试(得分均为整数),成绩满分为
名学生进行了一次体育模拟测试(得分均为整数),成绩满分为![]() 分,
分,![]() 班的体育委员根据这次测试成绩,制作了统计图和分析表如下:
班的体育委员根据这次测试成绩,制作了统计图和分析表如下:
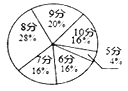
八年级![]() 班全体女生体育测试成绩分布扇形统计图
班全体女生体育测试成绩分布扇形统计图
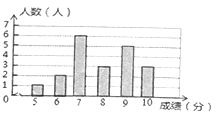
八年级全体男生体育测试成绩条形统计图
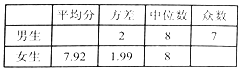
八年级![]() 班体育模拟测试成绩分析表
班体育模拟测试成绩分析表
根据以上信息,解答下列问题:
(1)这个班共有男生 人,共有女生 人;
(2)补全八年级![]() 班体育模拟测试成绩分析表;
班体育模拟测试成绩分析表;
(3)你认为在这次体育测试中,![]() 班的男生队,女生队哪个表现更突出一些?并写出你的看法的理由.
班的男生队,女生队哪个表现更突出一些?并写出你的看法的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com