练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

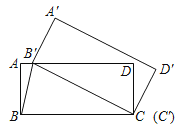
    【题目】如图，矩形ABCD中，BC＝4，将矩形ABCD绕点C顺时针旋转得到矩形A′B′C′D'．设旋转角为α，此时点B′恰好落在边AD上，连接B'B．

    （1）当B'恰好是AD中点时，此时α＝　 　；

    （2）若∠AB'B＝75°，求旋转角α及AB的长．

    【答案】（1）60°；

    （2）2．

    【解析】

    （1）作垂直BC于E，根据题意求出，CE=2，即可得出答案；

    （2）根据内角和求出∠ABB'，再根据余角求出∠CBB'＝75°，进而得到∠CBB'＝∠CB'B=75°，再求出∠BCB'，即可得出答案.

    解：（1）作垂直BC于E

    根据旋转性质可知，

    又B'恰好是AD中点

    ∴CE=2

    在直角三角形中，，CE=2

    ∴

    故

    （2）∵∠AB'B＝75°

    ∴∠ABB'＝15°

    ∴∠CBB'＝75°

    ∵

    ∴∠CBB'＝∠CB'B=75°

    ∴∠BCB'=180°-75°-75°=30°

    ∴

    ∴AB=2

    故旋转角α是30°，AB的长为2.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，直线l：y＝3x﹣3分别与x轴，y轴交于点A，点B，抛物线y＝ax2﹣2ax+a﹣4过点B．

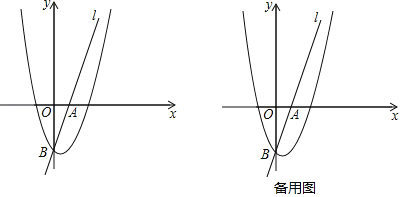
    （1）求抛物线的解析式；

    （2）点C是第四象限抛物线上一动点，连接AC，BC．

    ①当△ABC的面积最大时，求点C的坐标及△ABC面积的最大值；

    ②在①的条件下，将直线l绕着点A逆时针方向旋转到直线l'，l'与线段BC交于点D，设点B，点C到l'的距离分别为d1和d2，当d1+d2最大时，求直线l旋转的角度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校开展校园“美德少年”评选活动，共有“助人为乐”，“自强自立”、“孝老爱亲”，“诚实守信”四种类别，每位同学只能参评其中一类，评选后，把最终入选的20位校园“美德少年”分类统计，制作了如下统计表，后来发现，统计表中前两行的数据都是正确的，后两行的数据中有一个是错误的．

    类别

    频数

    频率

    助人为乐美德少年

    a

    0.20

    自强自立美德少年

    3

    b

    孝老爱亲美德少年

    7

    0.35

    诚实守信美德少年

    6

    0.32

    根据以上信息，解答下列问题：

    （1）统计表中的a＝　 　，b　 　；

    （2）统计表后两行错误的数据是　 　，该数据的正确值是　 　；

    （3）校园小记者决定从A，B，C三位“自强自立美德少年”中随机采访两位，用画树状图或列表的方法，求A，B都被采访到的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某兴趣小组借助无人飞机航拍校园．如图，无人飞机从A处水平飞行至B处需8秒，在地面C处同一方向上分别测得A处的仰角为75°，B处的仰角为30°．已知无人飞机的飞行速度为4米/秒，求这架无人飞机的飞行高度．（结果保留根号）

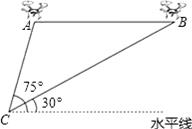
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校在“校园体育文化节”活动中组织了“球类知识我知道”的竞赛活动，从初三年级1200名学生中随机抽查了100名学生的成绩（满分30分），整理得到如下的统计图表：

    成绩（分）

    16

    17

    18

    19

    20

    21

    22

    23

    24

    25

    26

    27

    28

    29

    30

    人数

    1

    2

    3

    3

    6

    7

    5

    8

    15

    9

    11

    12

    8

    6

    4

    频率统计表

    成绩分组

    频数

    频率

    15≤x＜18

    3

    0.03

    18≤x＜21

    a

    0.12

    21≤x＜24

    20

    0.20

    24≤x＜27

    35

    0.35

    27≤x≤30

    30

    b

    频数分布直方图

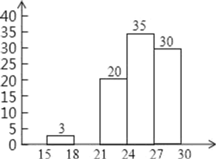
    请根据所提供的信息解答下列问题：

    （1）样本的众数是　 　分，中位数是　 　分；

    （2）频率统计表中a＝　 　，b＝　 　；补全频数分布直方图；

    （3）请根据抽样统计结果，估计该次竞赛中初三年级成绩不少于21分的大约有多少人？随机抽取一名同学的成绩，其值不小于24分的概率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，P是正三角形ABC内一点，且PA＝6，PB＝8，PC＝10，若将△PAC绕点A逆时针旋转后得到△P'AB．给出下列四个结论：①PP'＝6，②AP2+BP2＝CP2，③∠APB＝150°；④S△ABC＝36+25．正确结论个数为（　　）

    A.1B.2C.3D.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

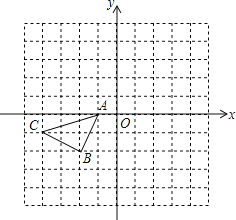
    【题目】如图所示的正方形网格中，△ABC的顶点均在格点上，请在所给直角坐标系中按要求画图和解答下列问题：

    （1）将△ABC沿x轴翻折后再沿x轴向右平移1个单位，在图中画出平移后的△A1B1C1．

    （2）作△ABC关于坐标原点成中心对称的△A2B2C2．

    （3）求B1的坐标　 　C2的坐标　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在一幅长为60 cm，宽为40 cm的矩形风景画的四周镶一条相同宽度的纸边，制成一幅矩形挂图．若要使整个挂图的面积是3 500 cm2，设纸边的宽为x cm，则根据题意可列方程为(　 　)

    A. (60＋x)(40＋x)＝3 500 B. (60＋2x)(40＋2x)＝3 500

    C. (60－x)(40－x)＝3 500 D. (60－2x)(40－2x)＝3 500

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明同学在一次社会实践活动中，通过对某种蔬菜在1月份至7月份的市场行情进行统计分析后得出如下规律：

    ①该蔬菜的销售价（单位：元/千克）与时间（单位：月份）满足关系： ；

    ②该蔬菜的平均成本（单位：元/千克）与时间（单位：月份）满足二次函数关系．已知4月份的平均成本为2元/千克，6月份的平均成本为1元/千克．

    （1）求该二次函数的解析式；

    （2）请运用小明统计的结论，求出该蔬菜在第几月份的平均利润（单位：元/千克）最大？最大平均利润是多少？（注：平均利润销售价平均成本）

    查看答案和解析>>

    同步练习册答案