
【题目】如图,直线l:y=3x﹣3分别与x轴,y轴交于点A,点B,抛物线y=ax2﹣2ax+a﹣4过点B.
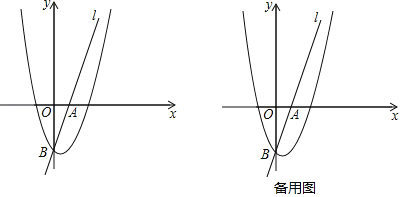
(1)求抛物线的解析式;
(2)点C是第四象限抛物线上一动点,连接AC,BC.
①当△ABC的面积最大时,求点C的坐标及△ABC面积的最大值;
②在①的条件下,将直线l绕着点A逆时针方向旋转到直线l',l'与线段BC交于点D,设点B,点C到l'的距离分别为d1和d2,当d1+d2最大时,求直线l旋转的角度.
【答案】(1)y=x2﹣2x﹣3;(2)①点C的坐标为(![]() ),△ABC面积的最大值为
),△ABC面积的最大值为![]() ;②直线l旋转的角度是45°
;②直线l旋转的角度是45°
【解析】
(1)利用直线l的解析式求出B点坐标,再把B点坐标代入二次函数解析式即可求出a的值,则抛物线的解析式的解析式可求出;
(2)①设C的坐标为(m,m2-2m-3),然后根据面积关系S△ABC=S四边形OACB-S△AOB可求出△ABC的面积,由二次函数的性质可求出△ABC面积的最大值及此时点C的坐标;
②如图2,过点B作BN垂直于l′于N点,过点C作CM垂直于l′于M点,则BN=d1,CM=d2,可将求d1+d2最大值转化为求AD的最小值.
(1)令x=0代入y=3x-3,
∴y=-3,
∴B(0,-3),
把B(0,-3)代入y=ax2-2ax+a-4,
∴-3=a-4,
∴a=1,
∴二次函数解析式为:y=x2-2x-3;
(2)如图1,连结OC,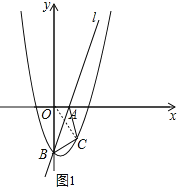
令y=0代入y=3x-3,
∴0=3x-3,
∴x=1,
∴A的坐标为(1,0),
由题意知:C的坐标为(m,m2-2m-3),
S△ABC=S四边形OACB-S△AOB
=S△OBC+S△OAC-S△AOB
=![]() ,
,
∴当m=![]() 时,S取得最大值,
时,S取得最大值,
当m=![]() 时,m2-2m-3=
时,m2-2m-3=![]() 53=
53=![]() ,
,
∴点C的坐标为(![]() ),△ABC面积的最大值为
),△ABC面积的最大值为![]() ;
;
(3)如图2,过点B作BN垂直于l′于N点,过点C作CM垂直于l′于M点,直线l'交BC于点D,则BN=d1,CM=d2,
∵S△ABC=![]() ×AD×(d1+d2)
×AD×(d1+d2)
当d1+d2取得最大值时,AD应该取得最小值,当AD⊥BC时取得最小值.
根据B(0,-3)和C(![]() )可得BC=
)可得BC=![]() ,
,
∵S△ABC=![]() ,
,
∴AD=![]() ,
,
当AD⊥BC时,cos∠BAD=![]() ,
,
∴∠BAD=45°.
即直线l旋转的角度是45°.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于圆O ,AD、BC的延长线相交于点E,AB、DC的延长线相交于点F.
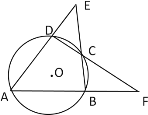
(1)若∠E=500, ∠F=400,求∠A的度数.
(2)探究∠E、∠F、∠A的关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角三角形ABC内接于⊙O,AD⊥BC,垂足为D.
(1)如图1, ![]() ,BD=DC,求∠B的度数;
,BD=DC,求∠B的度数;
(2)如图2,BE⊥AC,垂足为E,BE交AD于点F,过点B作BG∥AD交⊙O于点G,在AB边上取一点H,使得AH=BG.求证:△AFH是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=120°,AB=AC=6,D为边AB上一动点(不与B点重合),连接CD,将线段CD绕着点D逆时针旋转90°得到DE,连接BE,则S△BDE的最大值为_____.
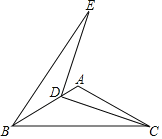
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】密闭容器内有一定质量的二氧化碳,当容器的体积V(单位:m3)变化时,气体的密度ρ(单位:kg/m3)随之变化,已知密度ρ与体积V是反比例函数关系,它的图象如图所示.
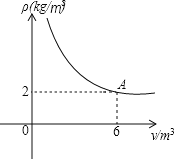
(1)求密度ρ关于体积V的函数解析式;
(2)当密度ρ不低于4kg/m3时,求二氧化碳体积的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“测量物体的高度” 活动中,某数学兴趣小组的3名同学选择了测量学校里的三棵树的高度.在同一时刻的阳光下,他们分别做了以下工作:
小芳:测得一根长为1米的竹竿的影长为0.8米,甲树的影长为4米(如图1).
小华:发现乙树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图2),墙壁上的影长为1.2米,落在地面上的影长为2.4米.
小丽:测量的丙树的影子除落在地面上外,还有一部分落在教学楼的第一级台阶上(如图3),测得此影子长为0.3米,一级台阶高为0.3米,落在地面上的影长为4.5米.

(1)在横线上直接填写甲树的高度为 米.
(2)求出乙树的高度.
(3)请选择丙树的高度为( )
A、6.5米 B、5. 5米 C、6.3米 D、4.9米
查看答案和解析>>
科目:初中数学 来源: 题型:
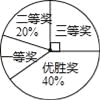
【题目】国务院办公厅在2015年3月16日发布了《中国足球发展改革总体方案》,这是中国足球史上的重大改革,为进一步普及足球知识,传播足球文化,我市某区在中小学举行了“足球在身边”知识竞赛,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题:
(1)获得一等奖的学生人数;
(2)在本次知识竞赛活动中,A,B,C,D四所学校表现突出,现决定从这四所学校中随机选取两所学校举行一场足球友谊赛,请用画树状图或列表的方法求恰好选到A,B两所学校的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
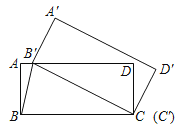
【题目】如图,矩形ABCD中,BC=4,将矩形ABCD绕点C顺时针旋转得到矩形A′B′C′D'.设旋转角为α,此时点B′恰好落在边AD上,连接B'B.
(1)当B'恰好是AD中点时,此时α= ;
(2)若∠AB'B=75°,求旋转角α及AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com