
【题目】密闭容器内有一定质量的二氧化碳,当容器的体积V(单位:m3)变化时,气体的密度ρ(单位:kg/m3)随之变化,已知密度ρ与体积V是反比例函数关系,它的图象如图所示.
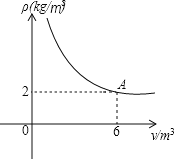
(1)求密度ρ关于体积V的函数解析式;
(2)当密度ρ不低于4kg/m3时,求二氧化碳体积的取值范围。
科目:初中数学 来源: 题型:
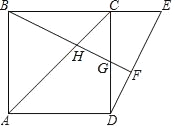
【题目】如图,点E是正方形ABCD的边BC延长线上一点,联结DE,过顶点B作BF⊥DE,垂足为F,BF交边DC于点G.
(1)求证:GDAB=DFBG;
(2)联结CF,求证:∠CFB=45°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C1:y=ax2+bx+b2向左平移1个单位长度,再向上平移4个单位长度得到抛物线C2:y=x2.
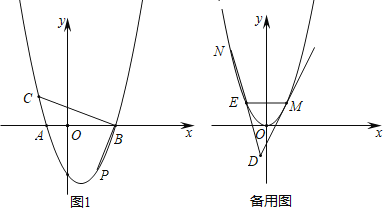
(1)直接写出抛物线C1的解析式;
(2)如图1,已知抛物线C1交x轴于点A、点B,点A在点B的左侧,点P(2,t)在抛物线C1上,CB⊥PB交抛物线于点C,求C点的坐标;
(3)已知点E、点M在抛物线C2上,EM∥x轴,点E在点M左侧,过点M的直线MD与抛物线C2只有一个公共点(MD与y轴不平行),直线DE与抛物线交于另一点N.若线段NE=DE,设点M、N的横坐标分别为m、n,求m和n的数量关系(用含m的式子表示n)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y=3x﹣3分别与x轴,y轴交于点A,点B,抛物线y=ax2﹣2ax+a﹣4过点B.
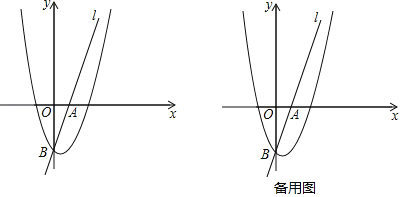
(1)求抛物线的解析式;
(2)点C是第四象限抛物线上一动点,连接AC,BC.
①当△ABC的面积最大时,求点C的坐标及△ABC面积的最大值;
②在①的条件下,将直线l绕着点A逆时针方向旋转到直线l',l'与线段BC交于点D,设点B,点C到l'的距离分别为d1和d2,当d1+d2最大时,求直线l旋转的角度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在研究相似问题时,甲、乙同学的观点如下:
甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形相似.
对于两人的观点,下列说法正确的是( )

A.甲对,乙不对 B.甲不对,乙对 C.两人都对 D.两人都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=![]() ,BC=12,E为AD中点,F为AB上一点,将△AEF沿EF折叠后,点A恰好落到CF上的点G处,则折痕EF的长是_______ .
,BC=12,E为AD中点,F为AB上一点,将△AEF沿EF折叠后,点A恰好落到CF上的点G处,则折痕EF的长是_______ .
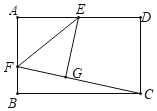
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(感知)如图①,在四边形![]() 中,点
中,点![]() 在边
在边![]() 上(点
上(点![]() 不与点
不与点![]() 、
、![]() 重合),
重合),![]() .易证:
.易证:![]() (不要求证明).
(不要求证明).
(探究)如图②,在四边形![]() 中,点
中,点![]() 在边
在边![]() 上(点
上(点![]() 不与点
不与点![]() 、
、![]() 重合),
重合),![]() .
.
(1)求证:![]() .
.
(2)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
(应用)如图③,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上(点
上(点![]() 不与点
不与点![]() 、
、![]() 重合),连结
重合),连结![]() ,作
,作![]() ,
,![]() 与边
与边![]() 交于点
交于点![]() .当
.当![]() 时,求
时,求![]() 的长.
的长.
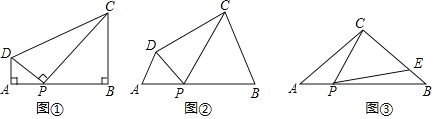
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是正三角形ABC内一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后得到△P'AB.给出下列四个结论:①PP'=6,②AP2+BP2=CP2,③∠APB=150°;④S△ABC=36+25![]() .正确结论个数为( )
.正确结论个数为( )

A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com