
����Ŀ����֪������C1��y��ax2+bx+b2����ƽ��1����λ���ȣ�������ƽ��4����λ���ȵõ�������C2��y��x2.
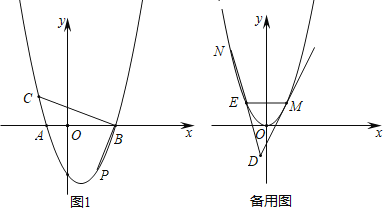
��1��ֱ��д��������C1�Ľ���ʽ��
��2����ͼ1����֪������C1��x���ڵ�A����B����A�ڵ�B����࣬��P��2��t����������C1�ϣ�CB��PB���������ڵ�C����C������ꣻ
��3����֪��E����M��������C2�ϣ�EM��x�ᣬ��E�ڵ�M��࣬����M��ֱ��MD��������C2ֻ��һ�������㣨MD��y�ƽ�У���ֱ��DE�������߽�����һ��N�����߶�NE��DE�����M��N�ĺ�����ֱ�Ϊm��n����m��n��������ϵ���ú�m��ʽ�ӱ�ʾn��
���𰸡���1��y����x��1��2��4����2��C����![]() ��
��![]() ������3��n����1
������3��n����1![]() ��m��
��m��
��������
��1��������C2��y��x2����ƽ��1����λ���ȣ�������ƽ��4����λ���ȵõ�C1��������⣻
��2������B��y���ƽ����MN������C��CM��MN�ڵ�M������P��PN��MN�ڵ�N��֤����BCM����PBN����tan��MCB��tan��PBN��![]() ����BM��m����CM��3m���ɵõ�C��3��3m��m��������C���������C1�Ľ���ʽ��������⣻
����BM��m����CM��3m���ɵõ�C��3��3m��m��������C���������C1�Ľ���ʽ��������⣻
��3��������ɵõ�M��N������Ϊ����m��m2������n��n2������E����m��m2������ֱ��MD�ı���ʽΪ��y��kx+b�������M�����겢����ֱ��MD��������C2ֻ��һ������������ֱ��MD�ı���ʽΪ��y��2mx��m2��Ȼ�����е����깫ʽ��ϵ�N��E�����꣬��ʾ����D�����꣬�ٽ���D���������ֱ��MD�ı���ʽ������⼴�ɣ�
��1��������C2��y��x2����ƽ��1����λ���ȣ�������ƽ��4����λ���ȵõ�C1��
��������C1�Ľ���ʽΪ��y����x��1��2��4��
��2������B��y���ƽ����MN������C��CM��MN�ڵ�M������P��PN��MN�ڵ�N��
�ߡ�PBN+��BPN��90������PBN+��CBM��90����
���BCM����PBN��
��y=0ʱ������x��1��2��4��0��
��ã�x=3��x=��1��
��B��3��0����
��x=2ʱ��y����x��1��2��4����3��
���P����������2����3������NB��3��PN��1��
��tan��MCB��tan��PBN��![]() ��
��
��BM��m����CM��3m�����C��3��3m��m����
����C���������C1�Ľ���ʽ�ɵã�m����3��3m��1��2��4
��ã�m��![]() ��m=0����ȥ������ʱ3��3m��
��m=0����ȥ������ʱ3��3m��![]() ��
��
�ʵ�C����![]() ��
��![]() ����
����
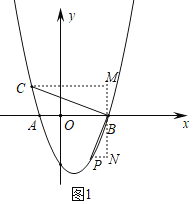
��3���ߵ�M��N�ĺ�����ֱ�Ϊm��n��
���M��N����������m��m2������n��n2�������E����m��m2����
��ֱ��MD�ı���ʽΪy��kx+b��
����M����������m2=km+b����b=m2��km��
��ֱ��MD�ı���ʽΪ��y��kx+m2��km��
����y��kx+m2��km��y��x2�ɵã�x2��kx+m2��km�������ã�x2��kx��m2��km��0��
��ֱ��MD��������C2ֻ��һ�������㣬
����������k��2��4����m2+km����k2+4m2��4km��0��
��ã�k��2m��
��ֱ��MD�ı���ʽΪ��y��2mx��m2��
��N��n��n2����E����m��m2����
�����е㹫ʽ�ã���D������Ϊ����2m��n����D������Ϊ��2m2��n2��
��D����2m��n��2m2��n2����
����D���������y��2mx��m2�ɵ�2m2��n2��2m(��2m��n) ��m2��
�����ã�n2��2mn��7m2��0��
��������ͬʱ����m2�ã�![]() ��
��
��ã�![]() ��
��
��n��![]() ��
��


 ��У��������ĩ��̾�ϵ�д�
��У��������ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
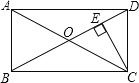
����Ŀ����ͼ���ھ���ABCD�У�BC��10���Խ���AC��BD�ཻ�ڵ�O��CE��BD������ΪE��BE��3DE����CE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������һ�����͵��Ӳ�Ʒ������ʱÿ���ijɱ�Ϊ40Ԫ��ͨ���������֣�������![]() ���
���![]() �����۵���
�����۵���![]() Ԫ
Ԫ![]() ֮�����һ�κ�����ϵ����ͼ����ͼ��ʾ��
֮�����һ�κ�����ϵ����ͼ����ͼ��ʾ��
![]() ��y��x�ĺ�����ϵʽ��
��y��x�ĺ�����ϵʽ��
![]() ��۲��Ź涨�����ֵ��Ӳ�Ʒ���۵��۲��ó���ÿ��80Ԫ����ô�������۵���x��Ϊÿ������Ԫʱ������ÿ�»�õ�����
��۲��Ź涨�����ֵ��Ӳ�Ʒ���۵��۲��ó���ÿ��80Ԫ����ô�������۵���x��Ϊÿ������Ԫʱ������ÿ�»�õ�����![]() �����������Ƕ��٣�
�����������Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��C��D��B����O��ΪԲ�ģ�OA��Ϊ�뾶��Բ���ϣ� AC=CD=DB��AB��OC�ڵ�E����֤��AE=CD��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
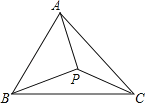
����Ŀ����ͼ���ȱ���ABC�У�AB��![]() ��3BP��4CP����BPC��120������ô�߶�AP�ij�����_____��
��3BP��4CP����BPC��120������ô�߶�AP�ij�����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������һ�ֶ�ͯ��ߣ�ÿ������20Ԫ���涨��������������10Ԫ���Ҳ�����18Ԫ���������ڼ䷢�֣������۵��۶�Ϊ35Ԫʱ��ÿ����۳�250�������۵���ÿ����1Ԫ��ÿ������������10�������������������ۣ���ÿ��������Ϊy�������۵���ΪxԪ��
��1����ֱ��д��y��x֮��ĺ�����ϵʽ���Ա���x��ȡֵ��Χ��
��2�������۵����Ƕ���Ԫʱ������ÿ�����3840Ԫ��
��3���������ÿ����1����ߣ��;���aԪ��0��a��6����ϣ�����̣�ÿ��۳�������ɻ���������Ϊ3300Ԫ����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ܱ���������һ�������Ķ�����̼�������������V����λ��m3���仯ʱ��������ܶ�������λ��kg/m3����֮�仯����֪�ܶ��������V�Ƿ�����������ϵ������ͼ����ͼ��ʾ.
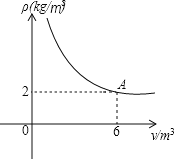
��1�����ܶ����������V�ĺ�������ʽ��
��2�����ܶ���������4kg/m3ʱ���������̼�����ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ʷ�ˮ����ƻ���![]() Ԫ/�еĽ��۹���һ��ˮ������Ա�����.
Ԫ/�еĽ��۹���һ��ˮ������Ա�����.
![]() �ݵ��飬������ˮ����е��ۼ�Ϊ
�ݵ��飬������ˮ����е��ۼ�Ϊ![]() Ԫ/��ʱ��������Ϊ
Ԫ/��ʱ��������Ϊ![]() �У�ÿ���ۼ�ÿ����
�У�ÿ���ۼ�ÿ����![]() Ԫ������������Ӧ����
Ԫ������������Ӧ����![]() �У���ʹˮ����е�������������
�У���ʹˮ����е�������������![]() �У�ÿ���ۼ�Ӧ�����ڶ���Ԫ?
�У�ÿ���ۼ�Ӧ�����ڶ���Ԫ?
![]() ��ʵ������ʱ�����������������ԭ��ÿ��ˮ����еĽ��������
��ʵ������ʱ�����������������ԭ��ÿ��ˮ����еĽ��������![]() ����ÿ��ˮ����е��ۼ۱�(1)������ۼۼ�����
����ÿ��ˮ����е��ۼ۱�(1)������ۼۼ�����![]() ����������(1)�����������
����������(1)�����������![]() ��������
��������![]() ���������ˮ�������۸�ˮ����е�����ﵽ��
���������ˮ�������۸�ˮ����е�����ﵽ��![]() Ԫ����
Ԫ����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ij����ֽƬABCD��EF��GH�۵�����E��H��AD���ϣ���F��G��BC���ϣ���ʹ�õ�B����C����AD����ͬһ��P����A��ĶԳƵ�Ϊ![]() �㣬D��ĶԳƵ�Ϊ
�㣬D��ĶԳƵ�Ϊ![]() �㣬��
�㣬��![]() ��
��![]() �����Ϊ4��
�����Ϊ4��![]() �����Ϊ1�������ABCD���������_____.
�����Ϊ1�������ABCD���������_____.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com