
����Ŀ��ij��������һ�ֶ�ͯ��ߣ�ÿ������20Ԫ���涨��������������10Ԫ���Ҳ�����18Ԫ���������ڼ䷢�֣������۵��۶�Ϊ35Ԫʱ��ÿ����۳�250�������۵���ÿ����1Ԫ��ÿ������������10�������������������ۣ���ÿ��������Ϊy�������۵���ΪxԪ��
��1����ֱ��д��y��x֮��ĺ�����ϵʽ���Ա���x��ȡֵ��Χ��
��2�������۵����Ƕ���Ԫʱ������ÿ�����3840Ԫ��
��3���������ÿ����1����ߣ��;���aԪ��0��a��6����ϣ�����̣�ÿ��۳�������ɻ���������Ϊ3300Ԫ����a��ֵ��
���𰸡���1��y����10x+600��30��x��38������2��36Ԫ����3��3.6
��������
��1������ԭ���ۼ�����ȥ���ٵļ�����Ϊ����
��2����������������ڵ����������������������⣻
��3�����ݵ��������ȥ������Ϊ��������ٸ�������������ڵ����������������������⣮
�⣺��1��������ã�y��250��10��x��35������10x+600��
��y��x֮��ĺ�����ϵʽΪ��y����10x+600��30��x��38����
��2��������������10x+600����x��20����3840��
��ã�x1��36��x2��44��
��30��x��38��
��x��36��
�𣺵����۵�����36Ԫʱ������ÿ�����3840Ԫ��
��3����ÿ��۳�������ɻ������ΪW��
��������ã�W������10x+600����x��20��a������10x2+��800+10a��x��600��20+a����
�߶Գ���x��40+![]() a��
a��
��30��x��38����0��a��6
��40��![]() a+40��43
a+40��43
��x��40+![]() aʱ��
aʱ��
ÿ��۳�������ɻ���������Ϊ3300Ԫ��
����10��40+![]() a��+600����40+
a��+600����40+![]() a��20��a����3300
a��20��a����3300
��200��5a����20��![]() a����3300
a����3300
������a2��80a+280��0
���a1��40��2![]() ��3.6��a2��40+2
��3.6��a2��40+2![]() ����ȥ����
����ȥ����
��a��ֵΪ3.6��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
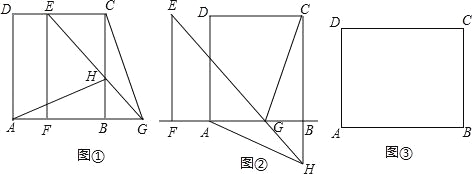
����Ŀ����֪���ھ���ABCD�У����ӶԽ���AC������ABC�Ƶ�B˳ʱ����ת90��õ���EFG����������ֱ��AB����ƽ�ƣ�ֱ��EG��BC���ڵ�H������AH��CG��
��1����ͼ������AB=BC����Fƽ�Ƶ��߶�BA��ʱ���߶�AH��CG��������������ϵ��λ�ù�ϵ��ֱ��д����IJ��룻
��2����ͼ������AB=BC����Fƽ�Ƶ��߶�BA���ӳ�����ʱ����1���еĽ����Ƿ��������˵�����ɣ�
��3����ͼ������AB=nBC��n��1��ʱ���Ծ���ABCD��������֪ͬ���ı任�������߶�AH��CG��������������ϵ��λ�ù�ϵ��ֱ��д����IJ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���C=90���� AD����BAC��ƽ���ߣ�O��AB��һ��, ��OAΪ�뾶����O������D��

��1����֤��BC����O���ߣ�
��2����BD=5��DC=3����AC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x�Ķ��κ���y��x2+bx+b2��b��x��b+3��Χ�ڣ�����ֵ����Сֵ21����b��ֵ�ǣ�������
A.![]() ��2
��2![]() B.
B.![]() ����2
����2![]() C.��4��
C.��4��![]() D.1��4��
D.1��4��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������C1��y��ax2+bx+b2����ƽ��1����λ���ȣ�������ƽ��4����λ���ȵõ�������C2��y��x2.
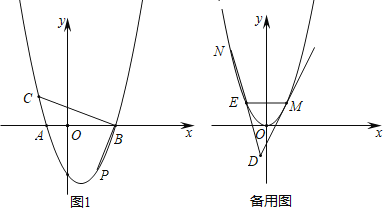
��1��ֱ��д��������C1�Ľ���ʽ��
��2����ͼ1����֪������C1��x���ڵ�A����B����A�ڵ�B����࣬��P��2��t����������C1�ϣ�CB��PB���������ڵ�C����C������ꣻ
��3����֪��E����M��������C2�ϣ�EM��x�ᣬ��E�ڵ�M��࣬����M��ֱ��MD��������C2ֻ��һ�������㣨MD��y�ƽ�У���ֱ��DE�������߽�����һ��N�����߶�NE��DE�����M��N�ĺ�����ֱ�Ϊm��n����m��n��������ϵ���ú�m��ʽ�ӱ�ʾn��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
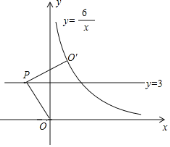
����Ŀ����ͼ����P��ֱ��y��3�ϵĶ��㣬����PO����PO��P����ת90����PO��������O���պ�����˫����![]() ��x��0����ʱ����P�ĺ��������п���ֵΪ_____��
��x��0����ʱ����P�ĺ��������п���ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����о���������ʱ���ס���ͬѧ�Ĺ۵����£�
�ף����߳�Ϊ3��4��5�������ΰ�ͼ1�ķ�ʽ�������ţ��õ��������Σ����ǵĶ�Ӧ���Ϊ1��������������ԭ���������ƣ�
�ң����ڱ�Ϊ3��5�ľ��ΰ�ͼ2�ķ�ʽ�������ţ��õ��µľ��Σ����ǵĶ�Ӧ����Ϊ1�����¾�����ԭ�������ƣ�
�������˵Ĺ۵㣬����˵����ȷ���ǣ� ��

A���ԣ��Ҳ��� B���ײ��ԣ��Ҷ� C�����˶��� D�����˶�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�Ķ��㶼�ڷ����ߵĽ��㣨��㣩�ϣ�
��1������ABC��C�㰴��ʱ�뷽����ת90��õ���A��B��C�䣬����ͼ�л�����A��B��C�䣮
��2������ABC����ƽ��1����λ��������ƽ��5����λ�õ���A��B��C�壬����ͼ�л�����A��B��C�壮
��3��������ABC��ԭ��O��ת180�㣬A�Ķ�Ӧ��A1�������� ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������κ���y=ax2+bx+c��a��0��ͼ��ĶԳ���Ϊx=1����y�ύ�ڵ�C����x�ύ�ڵ�A����B����1��0������
�ٶ��κ��������ֵΪa+b+c��
��a��b+c��0��
��b2��4ac��0��
�ܵ�y��0ʱ����1��x��3��������ȷ�ĸ����ǣ�������

A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com