
【题目】已知,在矩形ABCD中,连接对角线AC,将△ABC绕点B顺时针旋转90°得到△EFG,并将它沿直线AB向左平移,直线EG与BC交于点H,连接AH,CG.
(1)如图①,当AB=BC,点F平移到线段BA上时,线段AH,CG有怎样的数量关系和位置关系?直接写出你的猜想;
(2)如图②,当AB=BC,点F平移到线段BA的延长线上时,(1)中的结论是否成立,请说明理由;
(3)如图③,当AB=nBC(n≠1)时,对矩形ABCD进行如已知同样的变换操作,线段AH,CG有怎样的数量关系和位置关系?直接写出你的猜想.
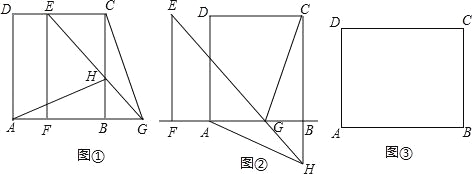
【答案】(1) AH=CG,AH⊥CG ;(2) 仍然成立,理由详见解析;(3) AH=nCG,AH⊥CG.理由详见解析.
【解析】
试题分析:(1)延长AH与CG交于点T,如图①,易证BH=BG,从而可证到△ABH≌△CBG,则有AH=CG,∠HAB=∠GCB,从而可证到∠HAB+∠AGC=90°,进而可证到AH⊥CG.
(2)延长CG与AH交于点Q,如图②,仿照(1)中的证明方法就可解决问题.
(3)延长AH与CG交于点N,如图③,易证BH∥EF,可得△GBH∽△GFE,则有![]() ,也就有
,也就有![]() ,从而可证到△ABH∽△CBG,则有
,从而可证到△ABH∽△CBG,则有![]() =n,∠HAB=∠GCB,进而可证到AH=nCG,AH⊥CG.
=n,∠HAB=∠GCB,进而可证到AH=nCG,AH⊥CG.
试题解析:(1)AH=CG,AH⊥CG.
证明:延长AH与CG交于点T,如图①,
由旋转和平移的性质可得:EF=AB,FG=BC,∠EFG=∠ABC.
∵四边形ABCD是矩形,AB=BC,
∴EF=GF,∠EFG=∠ABC=90°.
∴∠CBG=90°,∠EGF=45°.
∴∠BHG=90°﹣45°=45°=∠EGF.
∴BH=BG.
在△ABH和△CBG中,
AB=BC,∠ABH=∠CBG,BH=BG,
∴△ABH≌△CBG(SAS).
∴AH=CG,∠HAB=∠GCB.
∴∠HAB+∠AGC=∠GCB+∠AGC=90°.
∴∠ATC=90°.
∴AH⊥CG.
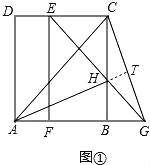
(2)(1)中的结论仍然成立.
证明:延长CG与AH交于点Q,如图②,
由旋转和平移的性质可得:EF=AB,FG=BC,∠EFG=∠ABC.
∵四边形ABCD是矩形,AB=BC,
∴EF=GF,∠EFG=∠ABC=90°.
∴∠ABH=90°,∠EGF=45°.
∴∠BGH=∠EGF=45°.
∴∠BHG=90°﹣45°=45°=∠BGH.
∴BH=BG.
在△ABH和△CBG中,
AB=BC,∠ABH=∠CBG,BH=BG,
∴△ABH≌△CBG(SAS).
∴AH=CG,∠HAB=∠GCB.
∴∠GCB+∠CHA=∠HAB+∠CHA=90°.
∴∠CQA=90°.
∴CG⊥AH.
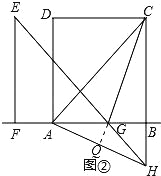
(3)AH=nCG,AH⊥CG.理由如下:
延长AH与CG交于点N,如图③,
由旋转和平移的性质可得:EF=AB,FG=BC,∠EFG=∠ABC.
∵四边形ABCD是矩形,AB=nBC,
∴EF=nGF,∠EFG=∠ABC=90°.
∴∠EFG+∠ABC=180°.
∴BH∥EF.
∴△GBH∽△GFE.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵∠ABH=∠CBG,
∴△ABH∽△CBG.
∴![]() =n,∠HAB=∠GCB.
=n,∠HAB=∠GCB.
∴AH=nCG,∠HAB+∠AGC=∠GCB+∠AGC=90°.
∴∠ANC=90°.
∴AH⊥CG.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(本题8分)已知△ABC的两边AB、AC的长恰好是关于x的方程x2+(2k+3)x+k2+3k+2=0的两个实数根,第三边BC的长为5
(1) 求证:AB≠AC
(2) 如果△ABC是以BC为斜边的直角三角形,求k的值
(3) 填空:当k=________时,△ABC是等腰三角形,△ABC的周长为________
查看答案和解析>>
科目:初中数学 来源: 题型:
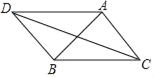
【题目】我们规定:等腰三角形的底角与顶角度数的比值叫做等腰三角形的“特征值”.如图,△ABC是以A为顶点的“特征值”为![]() 的等腰三角形,在△ABC外有一点D,若∠ADB=∠ABC,AD=4,BD=3,则∠ABC=_____度,CD的长是_____.
的等腰三角形,在△ABC外有一点D,若∠ADB=∠ABC,AD=4,BD=3,则∠ABC=_____度,CD的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
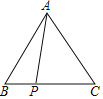
【题目】如图,△ABC中,AB=AC,∠B=60°,P是BC边上一点,将AP绕点A逆时针旋转60°,点P旋转后的对应点为P',连接CP'.
(1)画出旋转后示意图;
(2)连接PP',若∠BAP=20°,求∠PP'C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的内接三角形,P为BC延长线上一点,∠PAC=∠B,AD为⊙O的直径,过C作CG⊥AD于E,交AB于F,交⊙O于G.
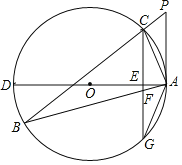
(1)判断直线PA与⊙O的位置关系,并说明理由;
(2)求证:AG2=AF·AB;
(3)求若⊙O的直径为10,AC=2![]() ,AB=4
,AB=4![]() ,求△AFG的面积.
,求△AFG的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数图象的顶点坐标是(3,5),且抛物线经过点A(1,3).
(1)求此抛物线的表达式;
(2)如果点A关于该抛物线对称轴的对称点是B点,且抛物线与y轴的交点是C点,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,∠A=60°,AB=6,扇形BEF的半径为6,圆心角为60°.
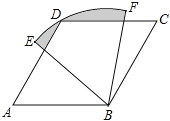
(1)连接DB,求证:∠DBF=∠ABE;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售一种儿童玩具,每件进价20元,规定单件销售利润不低于10元,且不高于18元.试销售期间发现,当销售单价定为35元时,每天可售出250件,销售单价每上涨1元,每天销售量减少10件,该网店决定提价销售.设每天销售量为y件,销售单价为x元.
(1)请直接写出y与x之间的函数关系式和自变量x的取值范围;
(2)当销售单价是多少元时,网店每天获利3840元?
(3)网店决定每销售1件玩具,就捐赠a元(0<a≤6)给希望工程,每天扣除捐赠后可获得最大利润为3300元,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com