
【题目】如图,△ABC的内接三角形,P为BC延长线上一点,∠PAC=∠B,AD为⊙O的直径,过C作CG⊥AD于E,交AB于F,交⊙O于G.
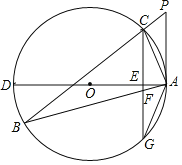
(1)判断直线PA与⊙O的位置关系,并说明理由;
(2)求证:AG2=AF·AB;
(3)求若⊙O的直径为10,AC=2![]() ,AB=4
,AB=4![]() ,求△AFG的面积.
,求△AFG的面积.
【答案】(1)见解析;(2)见解析;(3)3.
【解析】
(1)首先连接CD,由AD为⊙O的直径,可得∠ACD=90°,然后由圆周角定理,证得∠B=∠D,由已知∠PAC=∠B,可证得DA⊥PA,继而可证得PA与⊙O相切.
(2)首先连接BG,易证得△AFG∽△AGB,然后由相似三角形的对应边成比例,证得结论;
(3)首先连接BD,由AG2=AFAB,可求得AF的长,易证得△AEF∽△ABD,即可求得AE的长,继而可求得EF与EG的长,则可求得答案.
(1)PA与⊙O相切.理由:
如图1,连接CD,
∵AD为⊙O的直径,
∴∠ACD=90°,
∴∠D+∠CAD=90°,A
∵∠B=∠D,∠PAC=∠B,
∴∠PAC=∠D,
∴∠PAC+∠CAD=90°,
即DA⊥PA,
∵点A在圆上,
∴PA与⊙O相切.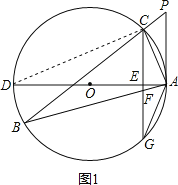
(2)
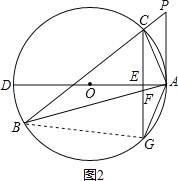
证明:如图2,连接BG,
∵AD为⊙O的直径,CG⊥AD,
∴![]() ,
,
∴∠AGF=∠ABG,
∵∠GAF=∠BAG,
∴△AGF∽△ABG,
∴AG:AB=AF:AG,
∴AG2=AFAB;
(3)
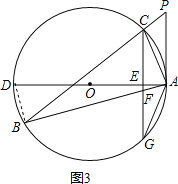
解:如图3,连接BD,
∵AD是直径,
∴∠ABD=90°,
∵AG2=AFAB,AG=AC=2![]() ,AB=4
,AB=4![]() ,
,
∴AF=![]() =
=![]() ,
,
∵CG⊥AD,
∴∠AEF=∠ABD=90°,
∵∠EAF=∠BAD,
∴△AEF∽△ABD,
∴![]() ,
,
即![]() ,
,
解得:AE=2,
∴EF=![]() =1,
=1,
∵EG=![]() =4,
=4,
∴FG=EG-EF=4-1=3,
∴S△AFG=![]() FGAE=
FGAE=![]()
![]() 3×3×2=3.
3×3×2=3.


科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中放有四张分别写有数字1、2、3、4的红色卡片和三张分别写有数字1、2、3的蓝色卡片,卡片除颜色和数字外其它完全相同。
(1)从中任意抽取一张卡片,则该卡片上写有数字1的概率是;
(2)将3张蓝色卡片取出后放入另外一个不透明的盒子内,然后在两个盒子内各任意抽取一张卡片,以红色卡片上的数字作为十位数,蓝色卡片上的数字作为个位数组成一个两位数,求这个两位数大于22的概率。(请利用树状图或列表法说明)
查看答案和解析>>
科目:初中数学 来源: 题型:
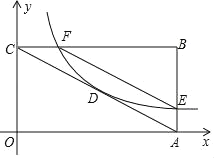
【题目】如图,在平面直角坐标系中,矩形OABC的两边分别在x轴、y轴上,D是对角线的交点,若反比例函数y=![]() 的图象经过点D,且与矩形OABC的两边AB,BC分别交于点E,F.
的图象经过点D,且与矩形OABC的两边AB,BC分别交于点E,F.
(1)若D的坐标为(4,2)
①则OA的长是 ,AB的长是 ;
②请判断EF是否与AC平行,井说明理由;
③在x轴上是否存在一点P.使PD+PE的值最小,若存在,请求出点P的坐标及此时PD+PE的长;若不存在.请说明理由.
(2)若点D的坐标为(m,n),且m>0,n>0,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
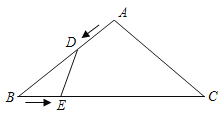
【题目】如图所示,在等腰△ABC中,AB=AC=10cm,BC=16cm.点D由点A出发沿AB方向向点B匀速运动,同时点E由点B出发沿BC方向向点C匀速运动,它们的速度均为1cm/s.连接DE,设运动时间为t(s)(0<t<10),解答下列问题:
(1)当t为何值时,△BDE的面积为7.5cm2;
(2)在点D,E的运动中,是否存在时间t,使得△BDE与△ABC相似?若存在,请求出对应的时间t;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
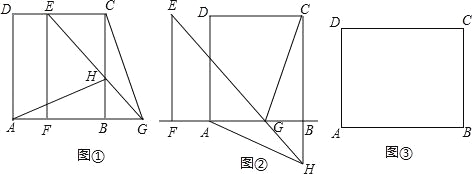
【题目】已知,在矩形ABCD中,连接对角线AC,将△ABC绕点B顺时针旋转90°得到△EFG,并将它沿直线AB向左平移,直线EG与BC交于点H,连接AH,CG.
(1)如图①,当AB=BC,点F平移到线段BA上时,线段AH,CG有怎样的数量关系和位置关系?直接写出你的猜想;
(2)如图②,当AB=BC,点F平移到线段BA的延长线上时,(1)中的结论是否成立,请说明理由;
(3)如图③,当AB=nBC(n≠1)时,对矩形ABCD进行如已知同样的变换操作,线段AH,CG有怎样的数量关系和位置关系?直接写出你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
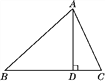
【题目】如图,在△ABC中,AD是BC边上的高,tanB=cos∠DAC.
(1)求证:AC=BD;
(2)若sin C=![]() ,BC=12,求△ABC的面积.
,BC=12,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中放入一个矩形纸片ABCO,将纸片翻折后,点B恰好落在![]() 轴上,记为
轴上,记为![]() ,折痕为CE.直线CE的关系式是
,折痕为CE.直线CE的关系式是![]() ,与
,与![]() 轴相交于点F,且AE=3.
轴相交于点F,且AE=3.
(1)求OC长度;
(2)求点![]() 的坐标;
的坐标;
(3)求矩形ABCO的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:如图①,在四边形ADBC中,∠ACB=∠ADB=90°,AD=BD,探究线段AC、BC、CD之间的数量关系.
小吴同学探究此问题的思路是:将ΔBCD绕点D逆时针旋转90°到ΔAED处,点B、C分别落在点A、E处(如图②),易证点C、A、E在同一条直线上,并且ΔCDE是等腰直角三角形,所以CE=![]() CD,从而得出结论:AC+BC=
CD,从而得出结论:AC+BC=![]() CD.
CD.




图① 图② 图③ 图④
简单应用:
(1)在图①中,若AC=![]() ,BC=2
,BC=2![]() ,则CD= .
,则CD= .
(2)如图③,AB是⊙O的直径,点C、D在⊙O上,弧AD=弧BD,若AB=13,BC=12,求CD的长.
拓展延伸:
(3)如图④,∠ACB=∠ADB=90°,AD=BD,若AC=m,BC=n(m<n),求CD的长(用含m,n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
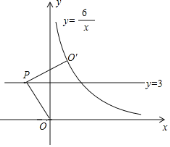
【题目】如图,点P是直线y=3上的动点,连接PO并将PO绕P点旋转90°到PO′,当点O′刚好落在双曲线![]() (x>0)上时,点P的横坐标所有可能值为_____.
(x>0)上时,点P的横坐标所有可能值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com