
【题目】如图,已知MN是⊙O的直径,直线PQ与⊙O相切于P点,NP平分∠MNQ. 
(1)求证:NQ⊥PQ;
(2)若⊙O的半径R=2,NP= ![]() ,求NQ的长.
,求NQ的长.
【答案】
(1)证明:连结OP,如图,
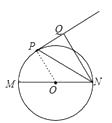
∴直线PQ与⊙O相切,
∴OP⊥PQ,
∵OP=ON,
∴∠ONP=∠OPN,
∵NP平分∠MNQ,
∴∠ONP=∠QNP,
∴∠OPN=∠QNP,
∴OP∥NQ,
∴NQ⊥PQ
(2)解:连结PM,如图,
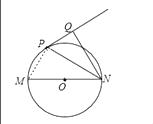
∵MN是⊙O的直径,
∴∠MPN=90°,
∵NQ⊥PQ,
∴∠PQN=90°,
而∠MNP=∠QNP,
∴Rt△NMP∽Rt△NPQ,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴NQ=3.
【解析】(1)连结OP,根据切线的性质由直线PQ与⊙O相切得OP⊥PQ,再由OP=ON得到∠ONP=∠OPN,由NP平分∠MNQ得到∠ONP=∠QNP,利用等量代换得∠OPN=∠QNP,根据平行线的判定得OP∥NQ,所以NQ⊥PQ;(2)连结PM,根据圆周角定理由MN是⊙O的直径得到∠MPN=90°,易证得Rt△NMP∽Rt△NPQ,然后利用相似比可计算出NQ的长.


科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(k+1)x+2k﹣2=0.
(1)求证:此方程总有两个实数根;
(2)若此方程有一个根大于0且小于1,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
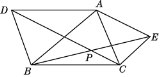
【题目】如图所示,在△ABC外作△ABD和△ACE,使AD=AB,AE=AC,且∠DAB=∠EAC,连接BE,CD相交于P点,求证:点A在∠DPE的平分线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
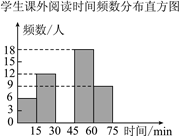
【题目】某校要了解学生每天的课外阅读时间情况,随机调查了部分学生,对学生每天的课外阅读时间x(单位:min)进行分组整理,并绘制了如图所示的不完整的统计图表,根据图中提供的信息,解答下列问题:
(1)本次调查共抽取了________名学生;
(2)统计表中a=________,b=________;
(3)将频数分布直方图补充完整;
(4)若全校共有1200名学生,请估计阅读时间不少于45 min的有多少人.
课外阅读时间x/min | 频数/人 | 百分比 |
0≤x<15 | 6 | 10% |
15≤x<30 | 12 | 20% |
30≤x<45 | a | 25% |
45≤x<60 | 18 | b |
60≤x<75 | 9 | 15% |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l和双曲线 ![]() (k>0)交于A,B两点,P是线段AB上的点(不与A,B重合),过点A,B,P分别向x轴作垂线,垂足分别是C,D,E,连接OA,OB,OP,设△AOC面积是S1 , △BOD面积是S2 , △POE面积是S3 , 则( )
(k>0)交于A,B两点,P是线段AB上的点(不与A,B重合),过点A,B,P分别向x轴作垂线,垂足分别是C,D,E,连接OA,OB,OP,设△AOC面积是S1 , △BOD面积是S2 , △POE面积是S3 , 则( ) 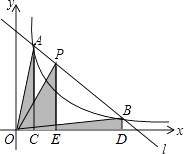
A.S1<S2<S3
B.S1>S2>S3
C.S1=S2>S3
D.S1=S2<S3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算或化简
(1)计算﹣14﹣(1﹣0.5)×![]() .
.
(2)计算(![]() )×(﹣36)+1+(﹣2)+|﹣2﹣3|﹣5.
)×(﹣36)+1+(﹣2)+|﹣2﹣3|﹣5.
(3)化简(3a﹣2b)+(5a﹣7b)﹣2(2a﹣4b).
(4)化简(﹣x2+2xy﹣y2)﹣2(xy﹣3x2)+3(2y2﹣xy).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=12cm,CE=5cm.则ABCD的周长为_____,面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】林城市对教师试卷讲评课中学生参与的深度和广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制了如图两幅不完整的统计图,请根据图中所给信息解答下列问题: 
(1)在这次评价中,一共抽查了名学生;
(2)请将条形统计图补充完整;
(3)如果全市有16万名初中学生,那么在试卷讲评课中,“独立思考”的学生约有多少万人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com