
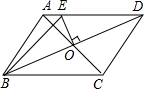
 如图所示,在四边形ABCD中,AB=DC,AD=BC,对角线AC,BD相交于点O,EO垂直平分BD,△ABE的周长为12cm,则四边形ABCD的周长为
如图所示,在四边形ABCD中,AB=DC,AD=BC,对角线AC,BD相交于点O,EO垂直平分BD,△ABE的周长为12cm,则四边形ABCD的周长为

科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,点0为坐标原点,△ABC的顶点B、C的坐标分别为(-2,O)、(3,O),顶点A在y轴的正半轴上,△ABC的高BD交线段DA于点E,且AD=BD.
如图,在平面直角坐标系中,点0为坐标原点,△ABC的顶点B、C的坐标分别为(-2,O)、(3,O),顶点A在y轴的正半轴上,△ABC的高BD交线段DA于点E,且AD=BD.查看答案和解析>>
科目:初中数学 来源: 题型:
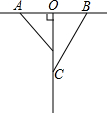 如图所示,AO=BO=50cm,OC是一条射线,OC⊥AB于点O,一只甲虫由点A以2cm/s的速度向B爬行,同时另一只甲虫由点O以3cm/s的速度沿OC方向爬行,是否存在这样的时刻,使两只甲虫与点O组成的三角形的面积为450cm2?若存在,请说明在什么时刻;若不存在,请说明理由.
如图所示,AO=BO=50cm,OC是一条射线,OC⊥AB于点O,一只甲虫由点A以2cm/s的速度向B爬行,同时另一只甲虫由点O以3cm/s的速度沿OC方向爬行,是否存在这样的时刻,使两只甲虫与点O组成的三角形的面积为450cm2?若存在,请说明在什么时刻;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF,其中正确的序号是
如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF,其中正确的序号是查看答案和解析>>
科目:初中数学 来源: 题型:
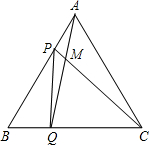 如图,点P、Q分别是边长是4cm的等边△ABC的边AB、BC上的动点,点P从顶点A出发沿着路线A→B→C→A做匀速运动,同时,点Q从顶点B出发,沿着路线B→C→A→B做匀速运动,且点P,Q的速度都为1cm/s,设运动时间为t秒
如图,点P、Q分别是边长是4cm的等边△ABC的边AB、BC上的动点,点P从顶点A出发沿着路线A→B→C→A做匀速运动,同时,点Q从顶点B出发,沿着路线B→C→A→B做匀速运动,且点P,Q的速度都为1cm/s,设运动时间为t秒查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com