
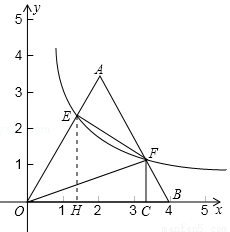
如图,将边长为4的等边三角形AOB放置于平面直角坐标系xOy中,F是AB边上的动点(不与点A,B重合),过点F的反比例函数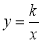 (
(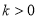 ,
,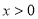 )与OA边交于点E,过点F作FC⊥x轴于点C,连接EF,OF.
)与OA边交于点E,过点F作FC⊥x轴于点C,连接EF,OF.

(1)若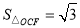 ,求反比例函数的解析式;
,求反比例函数的解析式;
(2)在(1)的条件下,试判断以点E为圆心,EA长为半径的圆与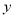 轴的位置关系,并说明理由;
轴的位置关系,并说明理由;
(3)AB边上是否存在点F,使得EF⊥AE?若存在,请求出BF:FA的值;若不存在,请说明理由.
(1)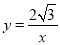 (
(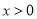 );(2)相离;(3)存在,1:4.
);(2)相离;(3)存在,1:4.
【解析】
试题分析:(1)设F(x,y),得到OC=x与CF=y,表示出三角形OCF的面积,求出xy的值,即为k的值,进而确定出反比例解析式;
(2)过E作EH垂直于x轴,EG垂直于y轴,设OH为m,利用等边三角形的性质及锐角三角函数定义表示出EH与OE,进而表示出E的坐标,代入反比例解析式中求出m的值,确定出EG,OE,EH的长,根据EA与EG的大小关系即可对于圆E与y轴的位置关系作出判断;
(3)过E作EH垂直于x轴,设FB=x,利用等边三角形的性质及锐角三角函数定义表示出FC与BC,进而表示出AF与OC,表示出AE与OE的长,得出OE与EH的长,表示出E与F坐标,根据E与F都在反比例图象上,得到横纵坐标乘积相等列出方程,求出方程的解得到x的值,即可求出BF与FA的比值.
试题解析:(1)设F(x,y),(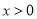 ,
,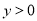 ),则OC=x,CF=y,∴
),则OC=x,CF=y,∴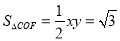 ,∴
,∴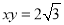 ,∴
,∴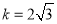 ,∴反比例函数解析式为
,∴反比例函数解析式为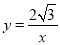 (
(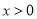 );
);
(2)该圆与y轴相离,理由为:过点E作EH⊥x轴,垂足为H,过点E作EG⊥y轴,垂足为G,
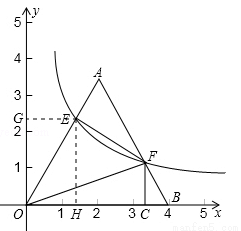
在△AOB中,OA=AB=4,∠AOB=∠ABO=∠A=60°,设OH=m,则tan∠AOB=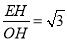 ,∴EH=
,∴EH=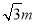 ,OE=2m,∴E坐标为(m,
,OE=2m,∴E坐标为(m,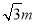 ),∵E在反比例
),∵E在反比例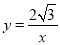 图象上,∴
图象上,∴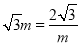 ,∴
,∴ ,
,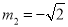 (舍去),∴OE=
(舍去),∴OE=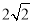 ,EA=
,EA=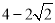 ,EG=
,EG=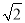 ,∵
,∵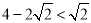 ,∴EA<EG,∴以E为圆心,EA长为半径的圆与y轴相离;
,∴EA<EG,∴以E为圆心,EA长为半径的圆与y轴相离;
(3)存在.假设存在点F,使AE⊥FE,过E点作EH⊥OB于点H,设BF=x.∵△AOB是等边三角形,∴AB=OA=OB=4,∠AOB=∠ABO=∠A=60°,∴BC=FBcos∠FBC=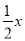 ,FC=FBsin∠FBC=
,FC=FBsin∠FBC=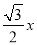 ,∴AF=4﹣x,OC=OB﹣BC=
,∴AF=4﹣x,OC=OB﹣BC=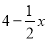 ,∵AE⊥FE,∴AE=AFcosA=
,∵AE⊥FE,∴AE=AFcosA=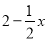 ,∴OE=OA﹣AE=
,∴OE=OA﹣AE=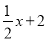 ,∴OH=OEcos∠AOB=
,∴OH=OEcos∠AOB=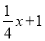 ,EH=OEsin∠AOB=
,EH=OEsin∠AOB=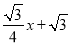 ,∴E(
,∴E(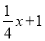 ,
,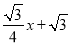 ),F(
),F(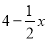 ,
,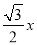 ),∵E、F都在双曲线
),∵E、F都在双曲线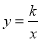 的图象上,∴(
的图象上,∴(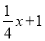 )(
)(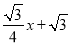 )=(
)=(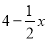 )
)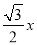 ,解得:
,解得: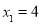 ,
,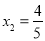 ,当BF=4时,AF=0,
,当BF=4时,AF=0,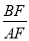 不存在,舍去;当BF=
不存在,舍去;当BF=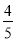 时,AF=
时,AF=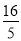 ,BF:AF=1:4.
,BF:AF=1:4.
考点:反比例函数综合题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
△ABC中,a,b,c分别是∠A,∠B,∠C的对边,如果a2+b2=c2,那么下列结论正确的是( )
A.csinA=a B.bcosB=c C.atanA=b D.ctanB=b
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省中山市九年级下学期开学检测数学试卷(解析版) 题型:选择题
下列说法正确的是( )
A.买福利彩票中奖,是必然事件. B.买福利彩票中奖,是不可能事件.
C.买福利彩票中奖,是随机事件. D.以上说法都正确.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省铜陵市四校九年级2月开学联考数学试卷(解析版) 题型:解答题
图中的小方格都是边长为1的正方形,△ABC的顶点和O点都在正方形的顶点上.
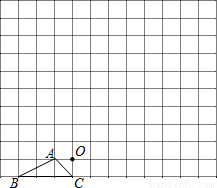
(1)以点O为位似中心,在方格图中将△ABC放大为原来的2倍,得到△A′B′C′;
(2)△A′B′C′绕点B′顺时针旋转90°,画出旋转后得到的△A″B′C″,并求边A′B′在旋转过程中扫过的图形面积.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省铜陵市四校九年级2月开学联考数学试卷(解析版) 题型:选择题
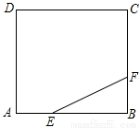
如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第n(n为正整数)次碰到点F时,小球P所经过的路程为( )
A.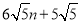 B.
B.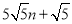 C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省安庆市九年级下学期正月联考数学试卷(解析版) 题型:解答题
如图,在平行四边形ABCD中,点G是BC延长线上一点,AG与BD交于点E,与DC交于点F,如果AB=m,CG=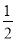 BC,求:
BC,求:
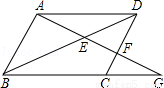
(1)DF的长度;
(2)三角形ABE与三角形FDE的面积之比.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省中山市七年级下学期开学检测数学试卷(解析版) 题型:解答题
(8分)在广州亚运会中,志愿者们手上、脖子上的丝巾非常美丽.车间70名工人承接了制作丝巾的任务,已知每人每天平均生产手上的丝巾1 800条或者脖子的丝巾1 200条,一条脖子上的丝巾要配两条手上的丝巾.为了使每天生产的丝巾刚好配套,应分配多少名工人生产脖子上的丝巾,多少名工人生产手上的丝巾?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com