
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
分析 首先根据点A(0,-3)是抛物线y=-(n-1)x2+n的最低点求出n的值,然后令y=0,求出x的值,进而求出抛物线与x轴两个交点之间的距离.
解答 解:∵点A(0,-3)是抛物线y=-(n-1)x2+n的最低点,
∴n=-3,
∴y=4x2-3,
∴令y=4x2-3=0,
∴x1=$\frac{\sqrt{3}}{2}$,x2=-$\frac{\sqrt{3}}{2}$,
∴x1-x2=$\frac{\sqrt{3}}{2}$-(-$\frac{\sqrt{3}}{2}$)=$\sqrt{3}$,
即抛物线与x轴两个交点之间的距离是$\sqrt{3}$,
故选C.
点评 本题主要考查了抛物线与x轴交点的知识,解答本题的关键是熟练掌握二次函数的性质以及顶点坐标的求法,此题难度不大,


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源:2016-2017学年吉林省七年级下学期期中数学模拟试卷(四)(解析版) 题型:解答题
先化简再求值 (2a+b)2﹣(3a﹣b)2+5a(a﹣b),其中a=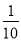 ,b=
,b=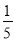 .
.
查看答案和解析>>
科目:初中数学 来源:2017届山东省中考模拟数学试卷(解析版) 题型:单选题
下列计算正确的是( )
A. a3+a2=a5 B. a3﹣a2=a C. a3•a2=a6 D. a3÷a2=a
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
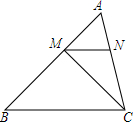 如图,△ABC中,BC=4,∠B=45°,AB=3$\sqrt{2}$,M、N分别是AB、AC上的点,MN∥BC.设MN=x,△MNC的面积为S.
如图,△ABC中,BC=4,∠B=45°,AB=3$\sqrt{2}$,M、N分别是AB、AC上的点,MN∥BC.设MN=x,△MNC的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
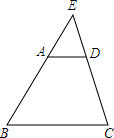 如图,在梯形ABCD中,AD∥BC,延长两腰交于点E,若AD=2,BC=6,AB=4,则$\frac{ED}{EC}$=$\frac{1}{3}$,$\frac{DE}{DC}$=$\frac{1}{2}$.
如图,在梯形ABCD中,AD∥BC,延长两腰交于点E,若AD=2,BC=6,AB=4,则$\frac{ED}{EC}$=$\frac{1}{3}$,$\frac{DE}{DC}$=$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com