
 如图,在△ABC中,AD是高,AE是角平分线,∠B=20°,∠C=60°.求∠CAD和∠AEC的度数.
如图,在△ABC中,AD是高,AE是角平分线,∠B=20°,∠C=60°.求∠CAD和∠AEC的度数. 分析 先根据三角形的高的定义得出∠ADC=90°,利用直角三角形两锐角互余可得∠CAD的度数;根据三角形内角和定理求出∠BAC,由三角形的角平分线定义求出∠BAE,再根据三角形外角的性质求出∠AEC的度数.
解答 解:∵在△ABC中,AD是高,
∴∠ADC=90°,
∵∠C=60°,
∴∠CAD=90°-∠C=30°;
∵∠B=20°,∠C=60°,
∴∠BAC=180°-∠B-∠C=100°,
∵AE是角平分线,
∴∠BAE=$\frac{1}{2}$∠BAC=50°,
∴∠AEC=∠B+∠BAE=20°+50°=70°.
点评 本题考查了三角形的角平分线、高的定义;三角形内角和定理以及推论,三角形外角的性质,熟练掌握三角形内角和定理,并能进行推理计算是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
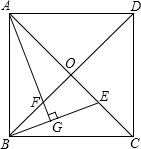 如图,已知正方形ABCD的对角线AC、BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.
如图,已知正方形ABCD的对角线AC、BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
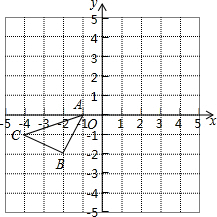 如图,所示的正方形网格中,△ABC的顶点均在格点上,在所给平面直角坐标系中解答下列问题:
如图,所示的正方形网格中,△ABC的顶点均在格点上,在所给平面直角坐标系中解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
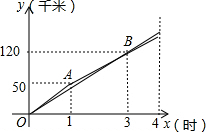 甲、乙两名自行车运动员在同一条直线公路上进行骑自行车训练,他们同时同地同向出发,乙在行驶过程中改变了一次速度,甲、乙两人各自在公路上训练时行驶路程y(千米)与行驶时间x(时)(0≤x≤4)之间的函数图象如图所示.
甲、乙两名自行车运动员在同一条直线公路上进行骑自行车训练,他们同时同地同向出发,乙在行驶过程中改变了一次速度,甲、乙两人各自在公路上训练时行驶路程y(千米)与行驶时间x(时)(0≤x≤4)之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}α+β=180\\ α=β-30\end{array}\right.$ | B. | $\left\{\begin{array}{l}α+β=180\\ α=β+30\end{array}\right.$ | C. | $\left\{\begin{array}{l}α+β=90\\ α=β+30\end{array}\right.$ | D. | $\left\{\begin{array}{l}α+β=90\\ α=β-30\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
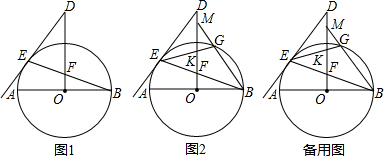
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com