
����Ŀ����ͼ����x����������A(m��0)��B(n��0)(n>m>0)���ֱ����A��B��x��Ĵ�
�߽�������y��x2�ڵ�C��D��ֱ��OC��ֱ��BD�ڵ�E��ֱ��OD��ֱ��AC�ڵ�F.��E��F��������ֱ�ΪyE��yF.
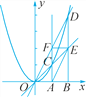
(1)����̽��(���)��
��m��1��n��2ʱ��yE��____��yF��____��
��m��3��n��5ʱ��yE��____��yF��____��
(2)����֤����������m,n(n>m>0)������yE��yF�Ĵ�С��ϵ����֤����IJ��룮
(3)��չӦ�ã�����EF��AE����S�ı���OFEB��3S��OFEʱ��ֱ��д��m��n�Ĺ�ϵ���ı���OFEA����״��
���𰸡�(1) ��m��1��n��2ʱ��yE��__2__�� ![]() ��__2__����m��3��n��5ʱ��
��__2__����m��3��n��5ʱ�� ![]() ��__15__��yF��__15__��
��__15__��yF��__15__��
(2) ![]() =
=![]() .֤����������
.֤����������
(3) n��2m,�ı���OFEAΪƽ���ı���.
����������������1����֪A��B�����꣬���������ߵĽ���ʽ���ܵõ�C��D�����꣬���������ֱ��OC��OD�Ľ���ʽ��Ҳ���ܵó�E��F��������꣬�ٽ��бȽϼ��ɣ���2����֪A��B�����꣬���������ߵĽ���ʽ���ܵõ�C��D�����꣬���������ֱ��OC��OD�Ľ���ʽ��Ҳ���ܵó�E��F��������꣬�ٽ��бȽϼ��ɣ���3���ı���OFEA������ɷ�����OEF����OEA�����֣����ݸ������ı��κ͡�OFE�����������ϵ�����жϳ�EF��OA�ı�����ϵ�������ó�m��n�ı�����ϵ���ٶ��ı���OFEA����״�����ж���
���������
(1) ��m��1��n��2ʱ��yE��__2__��yF��__2__����m��3��n��5ʱ��yE��__15__��yF��__15__.
(2)�ߵ�CΪ������y��x2�ϵĵ㣬AC��x�ᣬ��xC��xA��m�����C(m��m2)��
�����ֱ��yOC��mx��
�֡�xE��n����yE��mn.
ͬ������D(n��n2)�������ֱ��yOD��nx��
��yF��nm��mn.��yE��yF.
(3)��yE��yF��AF��x�ᣬBE��x�ᣬ
��AF��BE��AF��BE��
���ı���ABEFΪƽ���ı��Σ�
��EF��OB��EF��AB��n��m.
��S�ı���OFEB��![]() (n��m��n)��yE��
(n��m��n)��yE��![]() (2n��m)��yE��S��OFE��
(2n��m)��yE��S��OFE�� ![]() (n��m)��yE.
(n��m)��yE.
��S�ı���OFEB��3S��OFE��
��![]() (2n��m)��yE��3��
(2n��m)��yE��3��![]() (n��m)��yE��
(n��m)��yE��
��2n��m��3(n��m)����n��2m.
��ʱEF��n��m��2m��m��m��OA��
��EFƽ���ҵ���OA�����ı���OFEAΪƽ���ı��Σ�


 ����������ϵ�д�
����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽ�У���ȷ���У� ��
A.a3+a2��a5B.2a3a2��2a6
C.����2a3��2��4a6D.a8��a2��a4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x+y��2=12����x��y��2=4����x2+3xy+y2��ֵΪ��������
A.8B.10C.12D.14
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB��CD���ֱ�̽�������ĸ�ͼ���С�APC�͡�PAB����PCD�Ĺ�ϵ������������ĸ���ϵ��ѡ������һ����˵����̽���Ľ��۵���ȷ�ԣ�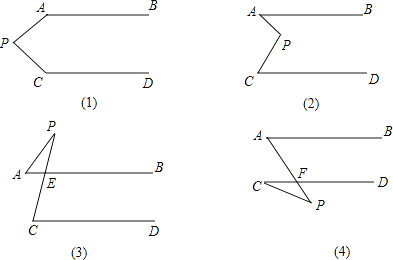
��1����
��2����
��3����
��4�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y��ax2(a��0)��ֱ��y��4x��3���ڵ�A(m��1)��
(1)���A�����꼰�����ߵĺ�������ʽ��(2)д�������ߵĿ��ڷ���������ͶԳ��ᣮ
(3)д��������y��ax2��ֱ��y��4x��3����һ������B�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����е�ʽ��������( )
A.(-x-1)2=(x-1)2B.(-x-1)2=(x+1)2
C.(-x+1)2=(x+1)2D.(x+1)2=(x-1)2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ�У�A��1��2����ĺ�����ˣ�1�������겻�䣬�õ�A���㣬��A��A���Ĺ�ϵ�ǣ� ��
A.����x��Գ� B.����y���
C.����ԭ��Գ� D.��A����x�Ḻ����ƽ��һ����λ
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com