
【题目】如图,已知AB∥CD,分别探究下面四个图形中∠APC和∠PAB、∠PCD的关系,请从你所得四个关系中选出任意一个,说明你探究的结论的正确性.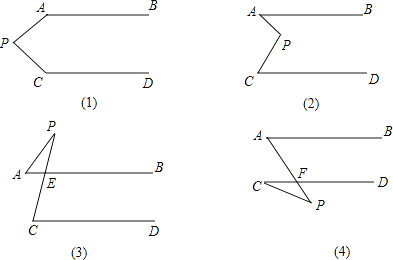
(1);
(2);
(3);
(4) .
【答案】
(1)∠APC+∠PAB+∠PCD=360°
(2)∠APC=∠BAP+∠DCP
(3)∠DCP=∠BAP+∠APC
(4)∠BAP=∠C+∠P
【解析】解:(1)连接AC,
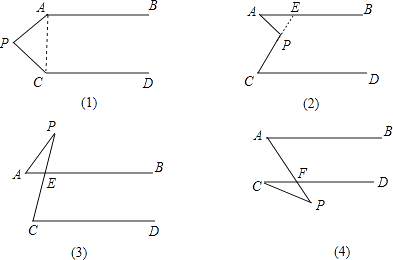
∵AB∥CD,
∴∠BAC+∠DCA=180°,
∵在△APC中,∠APC+∠PAC+∠PCA=180°,
∴∠APC+∠PAC+∠PCA+∠BAC+∠DCA=360°,
即∠APC+∠PAB+∠PCD=360°,
所以答案是:∠APC+∠PAB+∠PCD=360°;
⑵延长CP交AB于E,
∵AB∥CD,
∴∠DCP=∠AEP,
∵∠APC=∠BAP+∠AEP,
∴∠APC=∠BAP+∠DCP,
所以答案是:∠APC=∠BAP+∠DCP;
⑶∵AB∥CD,
∴∠DCP=∠BEP,
∵∠BEP=∠BAP+∠APC,
∴∠DCP=∠BAP+∠APC,
所以答案是:∠DCP=∠BAP+∠APC;
⑷∵AB∥CD,
∴∠BAP=∠DFP,
∵∠DFP=∠C+∠P
∴∠BAP=∠C+∠P
所以答案是∠BAP=∠C+∠P.
【考点精析】根据题目的已知条件,利用平行线的性质的相关知识可以得到问题的答案,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
【题目】直线y=﹣ ![]() x+3和x轴、y轴的交点分别为B、C,点A的坐标是(﹣
x+3和x轴、y轴的交点分别为B、C,点A的坐标是(﹣ ![]() ,0),另一条直线经过点A、C.
,0),另一条直线经过点A、C.
(1)求线段AC所对应的函数表达式;
(2)动点M从B出发沿BC运动,速度为1秒一个单位长度.当点M运动到C点时停止运动.设M运动t秒时,△ABM的面积为S.
①求S与t的函数关系式;
②当t为何值时,S= ![]() S△ABC , (注:S△ABC表示△ABC的面积),求出对应的t值;
S△ABC , (注:S△ABC表示△ABC的面积),求出对应的t值;
③当t=4的时候,在坐标轴上是否存在点P,使得△BMP是以BM为直角边的直角三角形?若存在,请直接写出P点坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了提升初中学生学习数学的兴趣,培养学生的创新精神,举办“玩转数学”比赛.现有甲、乙、丙三个小组进入决赛,评委从研究报告、小组展示、答辩三个方面为各小组打分,各项成绩均按百分制记录.甲、乙、丙三个小组各项得分如表:
小组 | 研究报告 | 小组展示 | 答辩 |
甲 | 91 | 80 | 78 |
乙 | 81 | 74 | 85 |
丙 | 79 | 83 | 90 |
(1)计算各小组的平均成绩,并从高分到低分确定小组的排名顺序;
(2)如果按照研究报告占40%,小组展示占30%,答辩占30%计算各小组的成绩,哪个小组的成绩最高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阜阳某企业今年1月份产值为a万元,2月份比1月份减少了10%,预计3月份比2月份增加15%.则3月份的产值将达到( )
A.(a﹣10%)(a+15%)万元
B.(a﹣10%+15%)万元
C.a(1﹣10%)(1+15%)万元
D.a(1﹣10%+15%)万元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从一副扑克牌中任意抽取1张.
①这张牌是“A”;
②这张牌是“红桃”;
③这张牌是“大王”;
④这张牌是“红色的”.
将这些事件按发生的可能性从小到大顺序排列 . (填序号,用“<”连接)
查看答案和解析>>
科目:初中数学 来源: 题型:
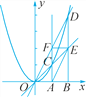
【题目】如图,在x轴上有两点A(m,0),B(n,0)(n>m>0),分别过点A,B作x轴的垂
线交抛物线y=x2于点C,D,直线OC交直线BD于点E,直线OD交直线AC于点F.点E,F的纵坐标分别为yE,yF.
(1)特例探究(填空):
当m=1,n=2时,yE=____,yF=____;
当m=3,n=5时,yE=____,yF=____.
(2)归纳证明:对任意m,n(n>m>0),猜想yE与yF的大小关系,并证明你的猜想.
(3)拓展应用:连结EF,AE,当S四边形OFEB=3S△OFE时,直接写出m与n的关系及四边形OFEA的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(﹣1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足(x+2)2+m≥kx+b的x的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com