
����Ŀ��ֱ��y=�� ![]() x+3��x�ᡢy��Ľ���ֱ�ΪB��C����A�������ǣ���
x+3��x�ᡢy��Ľ���ֱ�ΪB��C����A�������ǣ��� ![]() ��0������һ��ֱ�߾�����A��C��
��0������һ��ֱ�߾�����A��C��
��1�����߶�AC����Ӧ�ĺ�������ʽ��
��2������M��B������BC�˶����ٶ�Ϊ1��һ����λ���ȣ�����M�˶���C��ʱֹͣ�˶�����M�˶�t��ʱ����ABM�����ΪS��
����S��t�ĺ�����ϵʽ��
�ڵ�tΪ��ֵʱ��S= ![]() S��ABC �� ��ע��S��ABC��ʾ��ABC��������������Ӧ��tֵ��
S��ABC �� ��ע��S��ABC��ʾ��ABC��������������Ӧ��tֵ��
�۵�t=4��ʱ�������������Ƿ���ڵ�P��ʹ�á�BMP����BMΪֱ�DZߵ�ֱ�������Σ������ڣ���ֱ��д��P�����꣬�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��y=0ʱ���� ![]() x+3=0�����x=3
x+3=0�����x=3 ![]() ����B��3
����B��3 ![]() ��0��
��0��
��x=0ʱ��y=3����C�������ǣ�0��3��
���߶�AC����Ӧ�ĺ�������ʽy=kx+b��ͼ��A��C�㣬�� ![]() ��
��
��� ![]() ��
��
���߶�AC����Ӧ�ĺ�������ʽy= ![]() x+3
x+3
��2��
�⣺��ͼ1��
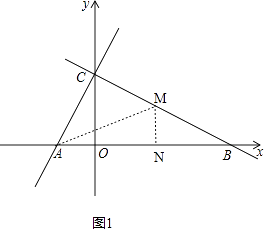
���ɶ���M��B������BC�˶����ٶ�Ϊ1��һ����λ���ȣ���ʻt�룬��BM=t��
���߶εĺͲ��AB=3 ![]() ������
������ ![]() ��=4
��=4 ![]() ��
��
�����������tan��B= ![]() =
= ![]() =
= ![]() ����ABC=30�㣬
����ABC=30�㣬
�����Һ�������MD=BMsin��ABC= ![]() t��
t��
�������������ʽ����S= ![]() ABMD=
ABMD= ![]() ��
�� ![]() t��4
t��4 ![]() =
= ![]() t
t
��S= ![]() t��
t��
����S= ![]() S��ABC����MD=
S��ABC����MD= ![]() OC=
OC= ![]() ����
���� ![]() t=
t= ![]() �����t=3��
�����t=3��
��t=3ʱ��S= ![]() S��ABC��
S��ABC��
����ͼ2��

��t=4ʱ�����������ϴ��ڵ�P��ʹ�á�BMP����BMΪֱ�DZߵ�ֱ�������Σ�
(i)��ͼ2��
�ߵ�M�˶����ٶ�Ϊÿ��1����λ���ȣ�
�൱t=4ʱ��BM=4��
�ߡ�ABC=30�㣬��PMB=90�㣬
��BP=BM��cos30��=4�� ![]() =
= ![]() ��
��
��OP=OB��BP=3 ![]() ��
�� ![]() =
= ![]() ��
��
���P�������ǣ� ![]() ��0����
��0����
(ii)��ͼ3��
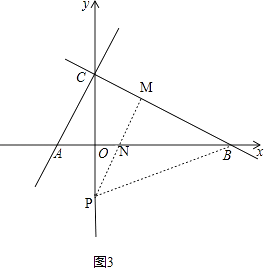
PM��AB�ཻ�ڵ�N����
�ߵ�M�˶����ٶ�Ϊÿ��1����λ���ȣ�
�൱t=4ʱ��BM=4��
�ߡ�ABC=30�㣬��NMB=90�㣬
��BN=BM��cos30��=4�� ![]() =
= ![]() ��
��
��ON=OB��BN=3 ![]() ��
�� ![]() =
= ![]() ��
��
�ߡ�MNB=90�㩁30��=60�㣬��ONP=��MNB��
���ONP=60�㣬
��OP=ONtan60��= ![]() =1��
=1��
���P�������ǣ�0����1����
(iii)��ͼ4��
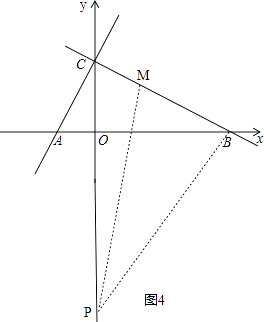
��OC=3����ABC=30�㣬��BOC=90�㣬
��BC=2��3=6����PCB=90�㩁30��=60�㣬
�֡ߡ�PBC=90�㣬
���BPC=90�㩁60��=30�㣬
��CP=2BC=2��6=12��
��OP=CP��OC=12��3=9��
���P�������ǣ�0����9����
���ϣ��ɵ�
��t=4ʱ�����������ϴ��ڵ�P��ʹ�á�BMP����BMΪֱ�DZߵ�ֱ�������Σ�
��P�������ǣ� ![]() ��0������0����1����0����9����
��0������0����1����0����9����
����������1�����ݺ���ֵ���ɵ���Ӧ�Ա�����ֵ�������Ա�����ֵ���ɵ���Ӧ�ĺ���ֵ�����ݴ���ϵ�������ɵú�������ʽ����2���ٸ���M���˶�ʱ�估�˶��ٶȣ��ɵ�BM�ij����������к���ֵ���ɵá�B�Ĵ�С���ٸ������Һ������ɵ�MD�ij��������߶εĺͲ�ɵ�AB�ij������������ε������ʽ���ɵô𰸣��ڸ��ݵȵ�������������S= ![]() S��ABC�Ĺ�ϵ���ɵ�MD=
S��ABC�Ĺ�ϵ���ɵ�MD= ![]() OB���ɵô𰸣��۸������⣬������������ٵ�P��x����ʱ���ڵ�P��y���ϣ���BPΪб��ʱ���۵�P��y���ϣ���BPΪ��һ��ֱ�DZ�ʱ��Ȼ�����ֱ�������ε����ʷ������ۣ����P��������Ƕ��ټ��ɣ�
OB���ɵô𰸣��۸������⣬������������ٵ�P��x����ʱ���ڵ�P��y���ϣ���BPΪб��ʱ���۵�P��y���ϣ���BPΪ��һ��ֱ�DZ�ʱ��Ȼ�����ֱ�������ε����ʷ������ۣ����P��������Ƕ��ټ��ɣ�
�����㾫����������Ĺؼ���������һ�κ��������ʵ����֪ʶ������һ��أ�һ�κ���y=kx+b���������ʣ���1����k>0ʱ��y��x�����������2����k<0ʱ��y��x���������С��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ж�����У��ڽǺ�����Ǻ͵�2�����ǣ� ��
A.������B.�����C.�ı���D.������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͬһƽ����������ֱ�ߣ����ֻ������ƽ�У���ô���ǽ���ĸ���Ϊ��������
A.0
B.1
C.2
D.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������˾��A��B�����ֿͳ������ǵ��ؿ�����������±���
A | B | |
�ؿ�������/���� | 45 | 30 |
���Ԫ/���� | 400 | 280 |
ѧУ����ʵ��������ƻ�����A��B�Ϳͳ���5����ͬʱ�Ͱ��꼶ʦ�������ʻ��زμ����ʵ�����������A�Ϳͳ�x��������Ҫ��ش���������:
��1���ú�x��ʽ����д�±���
������������ | �ؿ��� | ���Ԫ�� | |
A | x | 45x | 400x |
B | 5-x |
��2����Ҫ��֤����ò�����1900Ԫ�����������A�Ϳͳ���������
��3���ڣ�2���������£������꼶ʦ������195�ˣ�д�����п��ܵ����������ȷ����ʡǮ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������¼�Ϊ��Ȼ�¼����ǣ� ��
A.С���μӱ�����ѧ���ԣ��ɼ���150��
B.ij����˶�Ա���һ�Σ����а���
C.���ӻ���CCTV��һ��Ŀ���ڲ�������
D.�ڴ���װ��2�������1������������2�������б��к���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ
��1���뻭�� ![]() ����
���� ![]() ��ԳƵ�
��ԳƵ� ![]() ������
������ ![]() �ֱ���A,B,C�Ķ�Ӧ�㣬��д������
�ֱ���A,B,C�Ķ�Ӧ�㣬��д������
��2��ֱ��д�� ![]() ��������ꡣ
��������ꡣ
��3�����ABC������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽ�У���ȷ���У� ��
A.a3+a2��a5B.2a3a2��2a6
C.����2a3��2��4a6D.a8��a2��a4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ����(����)
A.x4+x4=x8B.x12��x4=x8C.x2x4=x8D.(x2)4=x8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB��CD���ֱ�̽�������ĸ�ͼ���С�APC�͡�PAB����PCD�Ĺ�ϵ������������ĸ���ϵ��ѡ������һ����˵����̽���Ľ��۵���ȷ�ԣ�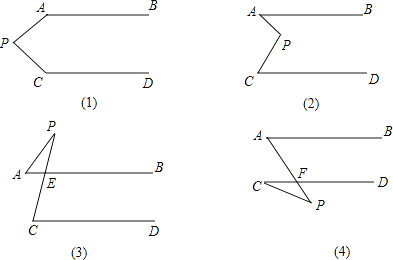
��1����
��2����
��3����
��4�� ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com