
【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A | B | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 400 | 280 |
学校根据实际情况,计划租用A、B型客车共5辆,同时送八年级师生到素质基地参加社会实践活动,设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆) | 载客量 | 租金(元) | |
A | x | 45x | 400x |
B | 5-x |
(2)若要保证租车费用不超过1900元,求最多租用A型客车多少辆?
(3)在(2)的条件下,若八年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案。
【答案】
(1)解:30(5-x)|280(5-x)
(2)解:根据题意,得400x+280(5-x)≤1900
解得x≤![]()
∴x的最大整数为4
答:最多租用A型客车4辆.
(3)解:由题意得,45x+30(5-x)≥195
解得x≥3
由(2)得,x≤ ![]()
∴3≤x≤ ![]() ∴x=3或4,
∴x=3或4,
∴有两种方案:①A型3辆,B型2辆,租车费用为400×3+280×2=1760(元)
②A型4辆,B型1辆,租车费用为400×4+280×1=1880(元)
所以符合题意的方案有两种,最省钱的方案是A型3辆,B型2辆。
【解析】(1)题中等量关系为:载客量=汽车数量![]() 每辆车载客量;租金=汽车数量
每辆车载客量;租金=汽车数量![]() 每辆车租金,据此列出表达式即可;(2)根据题意,得400x+280(5-x)≤1900,解出一元一次不等式,再求满足条件的最大整数解;(3)由45x+30(5-x)≥195解得x≥3及第(2)问x≤
每辆车租金,据此列出表达式即可;(2)根据题意,得400x+280(5-x)≤1900,解出一元一次不等式,再求满足条件的最大整数解;(3)由45x+30(5-x)≥195解得x≥3及第(2)问x≤ ![]() ,共同确定x的取值范围,进而得出所有可能的租车方案,比较出最省钱的租车方案.
,共同确定x的取值范围,进而得出所有可能的租车方案,比较出最省钱的租车方案.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】中国人最早开始使用负数,中国古代数学著作《九章算术》的‘方程’一章,在世界数学史首次正式引入负数. 如果增加400人记作+400,那么-360表示( )
A.增加40人B.减少360人C.增加360人D.减少40人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微笑的无花果,质量只有0.000000076克,将0.000000076克用科学记数法表示为( )
A.7.6×10﹣8
B.0.76×10﹣9
C.7.6×108
D.0.76×109
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是长方形,点A、C、D的坐标分别为A(9,0)、C(0,4),D(5,0),点P从点O出发,以每秒1个单位长度的速度沿O ![]() C
C ![]() B
B ![]() A运动,点P的运动时间为t秒.
A运动,点P的运动时间为t秒.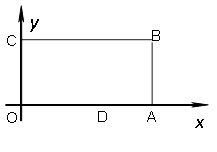
(1)当t=5时, P点坐标为( , )
(2)当t>4时,OP+PD有最小值吗?如果有,请算出该最小值,如果没有,请说明理由。
(3)当t为何值时,△ODP是腰长为5的等腰三角形?(直接写出t的值)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=﹣ ![]() x+3和x轴、y轴的交点分别为B、C,点A的坐标是(﹣
x+3和x轴、y轴的交点分别为B、C,点A的坐标是(﹣ ![]() ,0),另一条直线经过点A、C.
,0),另一条直线经过点A、C.
(1)求线段AC所对应的函数表达式;
(2)动点M从B出发沿BC运动,速度为1秒一个单位长度.当点M运动到C点时停止运动.设M运动t秒时,△ABM的面积为S.
①求S与t的函数关系式;
②当t为何值时,S= ![]() S△ABC , (注:S△ABC表示△ABC的面积),求出对应的t值;
S△ABC , (注:S△ABC表示△ABC的面积),求出对应的t值;
③当t=4的时候,在坐标轴上是否存在点P,使得△BMP是以BM为直角边的直角三角形?若存在,请直接写出P点坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com