
分析 (1)根据变形规律直接可以写出答案.
(2)根据规律展开即可化简求值.
解答 解:(1)$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
故答案为$\frac{1}{n}$-$\frac{1}{n+1}$
(2)原式=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2010}$-$\frac{1}{2011}$=1-$\frac{1}{2011}$=$\frac{2010}{2011}$.
故答案为$\frac{2010}{2011}$.
点评 本题考查分数的加法法则,运用规律把分数拆为两个分数的差是解题的关键.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:填空题
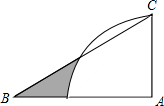 如图,Rt△ABC中,∠A=90°,∠B=30°,AC=6,以A为圆心,AC长为半径画四分之一圆,则图中阴影部分面积为9$\sqrt{3}$-3π.(结果保留π)
如图,Rt△ABC中,∠A=90°,∠B=30°,AC=6,以A为圆心,AC长为半径画四分之一圆,则图中阴影部分面积为9$\sqrt{3}$-3π.(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 小刚同学在一个正方体盒子的每个面都写了一个字,分别是:我、喜、欢、数、学、课.其平面展开图如图所示,那么在该正方体盒子中,和“我”相对的面所写的字是( )
小刚同学在一个正方体盒子的每个面都写了一个字,分别是:我、喜、欢、数、学、课.其平面展开图如图所示,那么在该正方体盒子中,和“我”相对的面所写的字是( )| A. | 课 | B. | 欢 | C. | 数 | D. | 学 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com