
����Ŀ����֪�ȱ�![]() �ı߳�Ϊ2���ֽ��ȱ�
�ı߳�Ϊ2���ֽ��ȱ�![]() ������ƽ��ֱ������ϵ�У���B��ԭ���غϣ���C��x���������ϣ�ֱ�߽�x���ڵ�D����y���ڵ�E����
������ƽ��ֱ������ϵ�У���B��ԭ���غϣ���C��x���������ϣ�ֱ�߽�x���ڵ�D����y���ڵ�E����![]() ��ͼ
��ͼ![]() ���ֽ��ȱ�
���ֽ��ȱ�![]() ��ͼ1��λ����x����������ÿ��1����λ���ȵ��ٶ��ƶ�����AB��AC�ֱ����߶�DE���ڵ�G��
��ͼ1��λ����x����������ÿ��1����λ���ȵ��ٶ��ƶ�����AB��AC�ֱ����߶�DE���ڵ�G��![]() ��ͼ
��ͼ![]() ��ͬʱ��P��
��ͬʱ��P��![]() �Ķ���B��������ÿ��2����λ���ȵ��ٶ�������
�Ķ���B��������ÿ��2����λ���ȵ��ٶ�������![]() �˶�
�˶�![]() ����P�˶���Cʱ��ֹͣ���
����P�˶���Cʱ��ֹͣ���![]() Ҳ��ֹ֮ͣ�ƶ�����
Ҳ��ֹ֮ͣ�ƶ�����![]() ƽ�Ƶ�ʱ��Ϊ
ƽ�Ƶ�ʱ��Ϊ![]() ��
��
![]() ����ֱ��DE�Ľ���ʽ��
����ֱ��DE�Ľ���ʽ��
![]() ����P���߶�AC���˶�ʱ�����P���H�ľ���Ϊy����y��t�ĺ�����ϵʽ����д��������
����P���߶�AC���˶�ʱ�����P���H�ľ���Ϊy����y��t�ĺ�����ϵʽ����д��������
![]() ����P���߶�AB���˶�ʱ��
����P���߶�AB���˶�ʱ��![]() ��ǡ����һ���ǵĶ���Ϊ
��ǡ����һ���ǵĶ���Ϊ![]() ����ֱ��д��t��ֵ������д���̣�
����ֱ��д��t��ֵ������д���̣�

���𰸡�![]() ���˶�ʱ��tΪ
���˶�ʱ��tΪ![]() ���
���![]() ���1��ʱ��
���1��ʱ��![]() ��ǡ����һ���ǵĶ���Ϊ
��ǡ����һ���ǵĶ���Ϊ![]()
��������
![]() ���ݵȱ������ε����ʽ��
���ݵȱ������ε����ʽ��![]() ���ɵó�
���ɵó�![]() �����AB�ij��ȿɵó�OE��OD�ij��ȣ������ɵó���D��E�����꣬���ô���ϵ�����������ֱ��DE�Ľ���ʽ��
�����AB�ij��ȿɵó�OE��OD�ij��ȣ������ɵó���D��E�����꣬���ô���ϵ�����������ֱ��DE�Ľ���ʽ��
![]() ���ݵ�P��C���˶��ٶȿɵó�PA��CD��ֵ����
���ݵ�P��C���˶��ٶȿɵó�PA��CD��ֵ����![]() ��
��![]() �ɵó�
�ɵó�![]() �������ɵó�CH�ij����ٸ���
�������ɵó�CH�ij����ٸ���![]() �����ҳ�y��t�ĺ�����ϵʽ��
�����ҳ�y��t�ĺ�����ϵʽ��
![]() �ֵ�P��A�غϼ���P��A���غ�����������ǣ�
�ֵ�P��A�غϼ���P��A���غ�����������ǣ�![]() ����P��A�غ�ʱ����
����P��A�غ�ʱ����![]() ʱ���������⣬��
ʱ���������⣬��![]() �����tֵ��
�����tֵ��![]() ����P��A���غ�ʱ����
����P��A���غ�ʱ����![]() ��
��![]() ����������ǣ�ͨ����ֱ�������μ������tֵ
����������ǣ�ͨ����ֱ�������μ������tֵ![]() ���ϼ��ɵó����ۣ�
���ϼ��ɵó����ۣ�
�⣺![]() Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ�
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��D������Ϊ
��D������Ϊ![]() ����E������Ϊ
����E������Ϊ![]()
��ֱ��DE�Ľ���ʽΪ![]() ��
��
��![]() ��
��![]() ����
����![]() ���ã�
���ã�
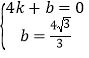 ����ã�
����ã�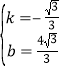 ��
��
![]() ֱ��DE�Ľ���ʽΪ
ֱ��DE�Ľ���ʽΪ![]() ��
��
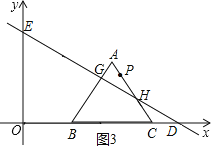
![]() ��ͼ3��
��ͼ3��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��P��AC�ϣ�
��P��AC�ϣ�
![]() ��
��
![]() ��
��
![]() ��ͼ2��
��ͼ2��![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ����P��A�غ�ʱ����
����P��A�غ�ʱ����![]() ʱ���������⣬
ʱ���������⣬
��ʱ![]() ��
��
![]() ����P��A���غ�ʱ��
����P��A���غ�ʱ��![]() ��
��![]() ��
��![]()
��![]() ����
����![]() ����
����![]() ��
��
��ã�![]() ��
��
��![]() ����
����![]() ����
����![]() ��
��
��ã�![]() ��
��
�������������˶�ʱ��tΪ![]() ���
���![]() ���1��ʱ��
���1��ʱ��![]() ��ǡ����һ���ǵĶ���Ϊ
��ǡ����һ���ǵĶ���Ϊ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij����֯20������װ����A��B��C������ȹ�100�ֵ�������ۣ����ƻ���20��������Ҫװ�ˣ�ÿ������ֻ��װ��ͬһ����ȣ��ұ���װ���������±��ṩ����Ϣ������������⣺

��1����װ��A����ȵij�����Ϊ![]() ��װ��B����ȵij�����Ϊ
��װ��B����ȵij�����Ϊ![]() ����
����![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��2�����װ��ÿ����ȵij�������������4������ô�����İ��ŷ����м��֣���д��ÿ�ְ��ŷ�����
��3����Ҫʹ�˴����ۻ������Ӧ�������ְ��ŷ������������������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�ǡ�ABC�����Բ����A=60�㣬����C����O�����ߣ�������BO�ڵ�E�� 
��1�����BCE�Ķ�����
��2������O�뾶Ϊ3����BE����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ƽ��ֱ������ϵxOy�У���A��x�Ḻ�����ϣ���B��y���������ϣ�OA=OB������y=�� ![]() ��ͼ�����߶�AB����M�㣬��AM=BM��
��ͼ�����߶�AB����M�㣬��AM=BM�� 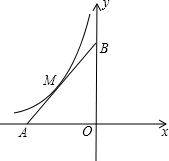
��1�����M�����ꣻ
��2����ֱ��AB�Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʵ�����ˮƽ�������мס��ҡ�������Բ���������������㹻�ߣ�������뾶֮��Ϊ1��2��1������������ͬ�Ĺ�����������5cm�߶ȴ���ͨ�������ӵ���������5cm���������������У�ֻ�м�����ˮ��ˮλ��1cm����ͼ��ʾ����ÿ����ͬʱ���Һͱ�ע����ͬ����ˮ����ʼעˮ1���ӣ��ҵ�ˮλ����![]() cm����ʼע�� ���ӵ�ˮ�������ҵ�ˮλ�߶�֮����0��5cm��
cm����ʼע�� ���ӵ�ˮ�������ҵ�ˮλ�߶�֮����0��5cm��
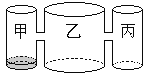
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����꼶(1)��ͬѧ����ѧ���,���ýdz�ƽ��һ����(��ͼ).��������·���:
(��)��AOB��һ�������,���dzߵ�ֱ�Ƕ���P��������OA,OB֮��,�ƶ��dz�ʹ�dz�������ͬ�Ŀ̶���M,N�غ�,��PM=PN,���dz߶���P������OP���ǡ�AOB��ƽ����.
(��)��AOB��һ�������,�ڱ�OA,OB�Ϸֱ�ȡOM=ON,���dzߵ�ֱ�Ƕ���P��������OA,OB֮��,�ƶ��dz�ʹ�dz�������ͬ�Ŀ̶���M,N�غ�,��PM=PN,���dz߶���P������OP���ǡ�AOB��ƽ����.
(1)����(��)������(��)�Ƿ����?������,��֤��;��������,��˵������.
(2)�ڷ���(��)PM=PN�������,�����ƶ��dz�,ͬʱʹPM��OA,PN��OB.�˷����Ƿ����?��˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ����ֲ�����Ϊ540 m2�ij��������������¢������ֲ�ݮ����������24¢����ֲ�IJ�ݮ������������ũ�������¢��������10¢���ֲ�����14¢(¢��Ϊ������)�����ǵ�ռ�����������������ֱ����£�

(1)�����ݮ����ֲ��x¢����˵�����м�����ֲ�������ֱ����ļ��֣�
(2)���⼸����ֲ�����У����ַ�����õ����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1����A��E��F��C��һ��ֱ���ϣ�AE=CF����E��F�ֱ���DE��AC��BF��AC����AB=CD����֤��BDƽ��EF��������DEC�ı�EC��AC�����ƶ���Ϊͼ��2��ʱ�������������䣬���������Ƿ��������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������л�ʫ�ʣ�Ѱ�Ļ�����Ʒ����֮������ijУ�ٰ����조�й�ʫ�ʴ�ᡱ����ѡ�κ���50��ѧ���μӾ�������50��ѧ��ͬʱĬд50��ʫ�ʣ���ÿ��ȷĬд��һ��ʫ�ʵ�2�֣����ݲ��Գɼ����Ƴ�����Ƶ���ֲ����Ͳ���Ƶ���ֲ�ֱ��ͼ��ͼ����
��� | �ɼ�x�� | Ƶ���������� |
��1�� | 50��x��60 | 6 |
��2�� | 60��x��70 | 8 |
��3�� | 70��x��80 | 14 |
��4�� | 80��x��90 | a |
��5�� | 90��x��100 | 10 |
����ͼ��������и��⣺
��1���������a��ֵ����Ƶ���ֲ�ֱ��ͼ����������
��2�������Գɼ�������80��Ϊ���㣬�β��Ե��������Ƕ��٣�
��3����5��10��ͬѧ�У���4����ͬѧ���ֽ���10��ͬѧƽ���ֳ�������жԿ���ϰ����4����ͬѧÿ������ˣ���С����Сǿ������ͬѧ�ܷ���ͬһ��ĸ��ʣ� 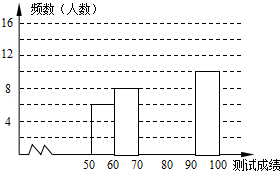
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com