
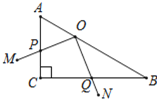
【题目】如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,直角∠MON的顶点O在AB上,OM、ON分别交CA、CB于点P、Q,∠MON绕点O意旋转.当![]() 时.
时.![]() 的值为_____.
的值为_____.
科目:初中数学 来源: 题型:
【题目】运城有甲、乙两家葡萄采摘园的葡萄销售价格相同,中秋期间,两家采摘园推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的葡萄六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘园的葡萄按售价付款。优惠期间,设游客的葡萄采摘量为![]() (千克),在甲园所需总费用为
(千克),在甲园所需总费用为![]() 甲(元),在乙园所需总费用为
甲(元),在乙园所需总费用为![]() 乙(元),
乙(元),![]() 甲,
甲,![]() 乙与
乙与![]() 之间的函数关系如图所示.
之间的函数关系如图所示.
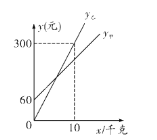
(1)求![]() 甲,
甲,![]() 乙与
乙与![]() 的函数表达式;
的函数表达式;
(2)在中秋期间,李娜一家三口准备去葡萄园采摘葡萄,采摘的葡萄合在一起支付费用,则李娜一家应选择哪家葡萄园更划算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (
(![]() 是常数,
是常数,![]() )的自变量
)的自变量![]() 与函数值
与函数值![]() 的部分对应值如下表:
的部分对应值如下表:
| … |
|
| 0 | 1 | 2 | … |
| … |
|
|
|
|
| … |
且当![]() 时,与其对应的函数值
时,与其对应的函数值![]() .有下列结论:①
.有下列结论:①![]() ;②
;②![]() 和3是关于
和3是关于![]() 的方程
的方程![]() 的两个根;③
的两个根;③![]()
![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,经过点C(0,﹣4)的抛物线![]() (
(![]() )与x轴相交于A(﹣2,0),B两点.
)与x轴相交于A(﹣2,0),B两点.

(1)a 0,![]() 0(填“>”或“<”);
0(填“>”或“<”);
(2)若该抛物线关于直线x=2对称,求抛物线的函数表达式;
(3)在(2)的条件下,连接AC,E是抛物线上一动点,过点E作AC的平行线交x轴于点F.是否存在这样的点E,使得以A,C,E,F为顶点所组成的四边形是平行四边形?若存在,求出满足条件的点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
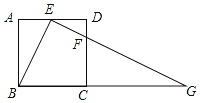
【题目】如图所示,在正方形ABCD中,E,F分别是边AD,CD上的点,AE=ED,DF=![]() DC,连结EF并延长交BC的延长线于点G,连结BE.
DC,连结EF并延长交BC的延长线于点G,连结BE.
(1)求证:△ABE∽△DEF.
(2)若正方形的边长为4,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A在x轴正半轴上,点B在y轴正半轴上,O为坐标原点,OA=OB=1,过点O作OM1⊥AB于点M1;过点M1作M1A1⊥OA于点A1:过点A1作A1M2⊥AB于点M2;过点M2作M2A2⊥OA于点A2…以此类推,点M2019的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
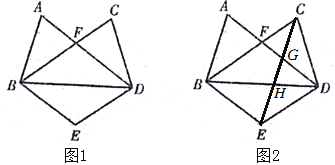
【题目】如图,AD与BC相交于点F,FA=FC,∠A=∠C,点E在BD的垂直平分线上.
(1)如图1,求证:∠FBE=∠FDE;
(2)如图2,连接CE分别交BD、AD于点H、G,当∠FBD=∠DBE=∠ABF,CD=DE时,直接写出所有与△ABF全等的三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】5G网络是第五代移动通信网络,它将推动我国数字经济发展迈上新台阶. 据预测,2020年到2030年中国5G直接经济产出和间接经济产出的情况如下图所示.
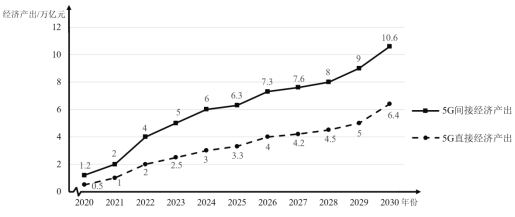
根据上图提供的信息,下列推断不合理的是( )
A.2030年5G间接经济产出比5G直接经济产出多4.2万亿元
B.2020年到2030年,5G直接经济产出和5G间接经济产出都是逐年增长
C.2030年5G直接经济产出约为2020年5G直接经济产出的13倍
D.2022年到2023年与2023年到2024年5G间接经济产出的增长率相同
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com