
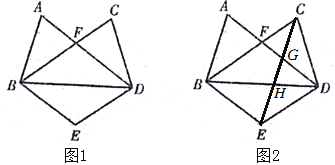
【题目】如图,AD与BC相交于点F,FA=FC,∠A=∠C,点E在BD的垂直平分线上.
(1)如图1,求证:∠FBE=∠FDE;
(2)如图2,连接CE分别交BD、AD于点H、G,当∠FBD=∠DBE=∠ABF,CD=DE时,直接写出所有与△ABF全等的三角形.
【答案】(1)证明见解析;(2)△DFC、△BEH、△CHD、△EDG.
【解析】试题分析:
(1)由题意易证△ABF≌△CDF,由此可得:BF=DF,从而可得∠FBD=∠FDB;由点E在BD的垂直平分线上可得BE=DE,由此可得∠EBD=∠EDB,这样即可得到∠FBE=∠FDE;
(2)由(1)中结论结合∠FBD=∠DBE=∠ABF,CD=DE易证△BFD≌△BED,由此可证得AB=CD=DE=BE=BF=DF,设∠ABF=2x,则可得∠A=∠BFA=90°-x,∠FBD=∠FDB=2x由此可得∠AFB=4x,这样在△ABF中由三角形内角和定理可得:2x+90-x+4x=180,由此可得x=18°,这样即可证得△ABF,△DCF,△BEH,△DEG和△CDH都是顶角为36°的等腰三角形,结合AB=CD=DE=BE即可得到这5个三角形全等,即与△ABF全等的三角形有4个.
试题解析:
(1)∵在△ABF和△CDF中,∠A=∠C,AF=CF,∠AFB=∠CFD,
∴△ABF≌△CDF,
∴BF=DF,
∴∠FBD=∠FDB,
∵由点E在BD的垂直平分线上,
∴BE=DE,
∴∠EBD=∠EDB,
∴∠FBD+∠EBD=∠FDB+∠EDB,即∠FBE=∠FDE;
(2)由(1)可知∠ABF=∠CDF,∠FBE=∠FDE,AB=CD,
∵∠FBD=∠DBE=∠ABF,CD=DE
∴∠ABF=∠FBD=∠EBD=∠CDF=∠FDB=∠BDE,AB=CD=DE=BE,
∴△BFD≌△BED,
∴BF=BE,
∴AB=BF=BE=DE=CD=DF,
∴若设∠ABF=2x,则可得∠A=∠AFB=90°-x,∠FBD=∠FDB=2x,
∵∠AFB=∠FBD+∠FDB=4x,
∴4x=90-x,解得x=18°,
由此可得∠ABF=2x=36°,∠A=∠AFB=72°,即△ABF是顶角为36°的等腰三角形,
结合∠ABF=∠FBD=∠EBD=∠CDF=∠FDB=∠BDE,AB=BF=BE=DE=CD=DF计算可得△DCF,△BEH,△DEG和△CDH都是顶角为36°的等腰三角形,且它们和△ABF有一腰是相等的,
∴△ABF,△DCF,△BEH,△DEG和△CDH是相互全等的,即与△ABF全等的三角形有4个,分别是△DCF,△BEH,△DEG和△CDH.


科目:初中数学 来源: 题型:
【题目】快递员小王下午骑摩托车从总部出发,在一条东西走向的街道上来回收送包裹.他行驶的情况记录如下(向东记为“![]() ”,向西记为“
”,向西记为“![]() ”,单位:千米):
”,单位:千米):
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)小王最后是否回到了总部?
(2)小王离总部最远是多少米?在总部的什么方向?
(3)如果小王每走![]() 米耗油
米耗油![]() 毫升,那么小王下午骑摩托车一共耗油多少毫升?
毫升,那么小王下午骑摩托车一共耗油多少毫升?
查看答案和解析>>
科目:初中数学 来源: 题型:
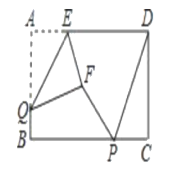
【题目】如图,矩形ABCD中,AB=4,BC=8,P,Q分别是直线BC,AB上的两个动点,AE=2,△AEQ沿EQ翻折形成△FEQ,连接PF,PD,则PF+PD的最小值是().
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举行“传承好家风”征文比赛,已知每篇参赛征文成绩记m分(60≤m≤100),组委会从1000篇征文中随机抽取了部分参赛征文,统计了他们的成绩,并绘制了如下不完整的两幅统计图表.

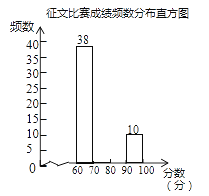
请根据以上信息,解决下列问题:
(1)征文比赛成绩频数分布表中c的值是________;
(2)补全征文比赛成绩频数分布直方图;
(3)若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别是A(-3,2),B(-1,4),C(0,2).
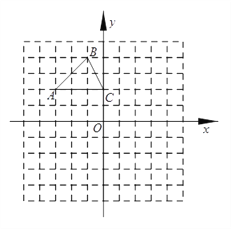
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;
(2)平移△ABC,若A的对应点A2的坐标为(-5,-2),画出平移后的△A2B2C2;
(3)若将△A2B2C2绕某一点旋转可以得到△A1B1C,请直接写出旋转中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
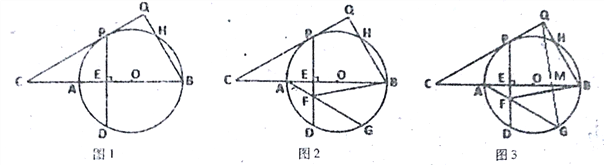
【题目】已知:如图,AB为⊙O的直径,C是BA延长线上一点,CP切⊙O于P,弦PD⊥AB于E,过点B作BQ⊥CP于Q,交⊙O于H.
(1)如图1,求证:PQ=PE;
(2)如图2,G是圆上一点,∠GAB=30![]() ,连接AG交PD于F,连接BF,tan∠BFE=
,连接AG交PD于F,连接BF,tan∠BFE=![]() ,求∠C的度数;
,求∠C的度数;
(3)如图3,在(2)的条件下,PD=6![]() ,连接QG交BC于点M,求QM的长.
,连接QG交BC于点M,求QM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( )
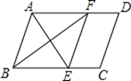
A. 13B. 14C. 15D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“幸福是奋斗出来的”,在数轴上,若C到A的距离刚好是3,则C点叫做A的“幸福点”,若C到A、B的距离之和为6,则C叫做A、B的“幸福中心”
(1)如图1,点A表示的数为﹣1,则A的幸福点C所表示的数应该是 ;
(2)如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为﹣2,点C就是M、N的幸福中心,则C所表示的数可以是 (填一个即可);
(3)如图3,A、B、P为数轴上三点,点A所表示的数为﹣1,点B所表示的数为4,点P所表示的数为8,现有一只电子蚂蚁从点P出发,以2个单位每秒的速度向左运动,当经过多少秒时,电子蚂蚁是A和B的幸福中心?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题:
大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用![]() -1来表示
-1来表示![]() 的小数部分,你同意小明的表示方法吗?
的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.
的整数部分是1,将这个数减去其整数部分,差就是小数部分.
又例如:∵![]() ,即
,即![]() ,
,
∴![]() 的整数部分为2,小数部分为(
的整数部分为2,小数部分为(![]() -2).
-2).
请解答:(1) ![]() 的整数部分是 ,小数部分是 .
的整数部分是 ,小数部分是 .
(2)如果![]() 的小数部分为a,
的小数部分为a, ![]() 的整数部分为b,求a+b-
的整数部分为b,求a+b-![]() 的值;
的值;
(3)已知: 10+![]() =x+y,其中x是整数,且0<y<1,求x-y的相反数.
=x+y,其中x是整数,且0<y<1,求x-y的相反数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com