
【题目】快递员小王下午骑摩托车从总部出发,在一条东西走向的街道上来回收送包裹.他行驶的情况记录如下(向东记为“![]() ”,向西记为“
”,向西记为“![]() ”,单位:千米):
”,单位:千米):
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)小王最后是否回到了总部?
(2)小王离总部最远是多少米?在总部的什么方向?
(3)如果小王每走![]() 米耗油
米耗油![]() 毫升,那么小王下午骑摩托车一共耗油多少毫升?
毫升,那么小王下午骑摩托车一共耗油多少毫升?
【答案】(1)是;(2)![]() 千米, 西;(3)
千米, 西;(3)![]() 毫升
毫升
【解析】
(1)根据有理数的加减法,再根据正负数即可;
(2)根据有理数的加减法,再根据正负数即可;
(3)根据绝对值的性质,再根据正负数即可;
(1)+2-3.5+3-4-2+2.5+2=0,
∴小王最后回到了总部;
(2)第一次离总部2=2千米;
第二次:2-3.5=-1.5千米;
第三次:-1.5+3=1.5千米;
第四次:1.5-4=-2.5千米;
第五次:-2.5-2=-4.5千米;
第六次:-4.5+2.5=-2千米;
第七次:-2+2=0千米.
所以离总部最远是4.5千米,在总部的西方向;
(3)|+2|+|-3.5|+|+3|+|-4|+|-2|+|+2.5|+|+2|=2+3.5+3+4+2+2.5+2=19千米
又∵摩托车每行驶1千米耗油30毫升,∴19×30=570(毫升)
∴这一天下午共耗油570毫升.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:
【题目】(1)一个两位数A,十位数字为a,个位数字为b,交换a和b的位置,得到一个新的两位数B,则A+B一定能被______整除,A-B一定能被______整除;
(2)一个三位数M,百位数字为a,十位数字为b,个位数字为c(a,b,c均为1至9的整数),交换a和c的位置,得到一个新的三位数N.请用含a、b、c的式子分别表示数N与M-N;
(3) 若(2)中a比b大1,M比N大792,求M.
查看答案和解析>>
科目:初中数学 来源: 题型:
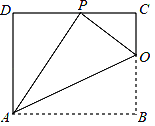
【题目】如图,已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的点P处,折痕与BC交于点O.
(1)求证:△OCP∽△PDA;
(2)若PO:PA=1:2,则边AB的长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格;
![]()
(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位运动员推铅球,铅球运行时离地面的高度![]() (米)是关于运行时间
(米)是关于运行时间![]() (秒)的二次函数.已知铅球刚出手时离地面的高度为
(秒)的二次函数.已知铅球刚出手时离地面的高度为![]() 米;铅球出手后,经过4秒到达离地面3米的高度,经过10秒落到地面.如图建立平面直角坐标系.
米;铅球出手后,经过4秒到达离地面3米的高度,经过10秒落到地面.如图建立平面直角坐标系.
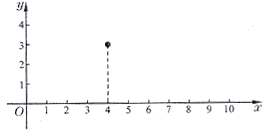
(Ⅰ)为了求这个二次函数的解析式,需要该二次函数图象上三个点的坐标.根据题意可知,该二次函数图象上三个点的坐标分别是____________________________;
(Ⅱ)求这个二次函数的解析式和自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a、b互为相反数,b、c互为倒数,并且m的立方等于它本身。
(1)求![]() +ac值.
+ac值.
(2)若a>1,且m<0,S=|2a-3b|-2|b-m|-|b+![]() |,求2a-S的值.
|,求2a-S的值.
(3)若m≠0,试讨论:x为有理数时|x+m|-|x-m|是否存在最大值?若存在求出这个最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+5(k为常数,且k≠0)的图象与反比例函数y=-![]() 的图象交于A(-2,b),B两点.
的图象交于A(-2,b),B两点.
(1)求一次函数的表达式;
(2)若将直线AB向下平移m(m>0)个单位长度后,与反比例函数的图象有且只有一个公共点,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
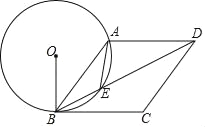
【题目】如图,点E在菱形ABCD的对角线BD上,连接AE,且AE=BE,⊙O是△ABE的外接圆,连接OB.
(1)求证:OB⊥BC;
(2)若BD=![]() ,tan∠OBD=2,求⊙O的半径.
,tan∠OBD=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
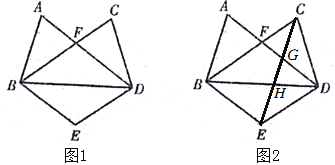
【题目】如图,AD与BC相交于点F,FA=FC,∠A=∠C,点E在BD的垂直平分线上.
(1)如图1,求证:∠FBE=∠FDE;
(2)如图2,连接CE分别交BD、AD于点H、G,当∠FBD=∠DBE=∠ABF,CD=DE时,直接写出所有与△ABF全等的三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com