
【题目】一位运动员推铅球,铅球运行时离地面的高度![]() (米)是关于运行时间
(米)是关于运行时间![]() (秒)的二次函数.已知铅球刚出手时离地面的高度为
(秒)的二次函数.已知铅球刚出手时离地面的高度为![]() 米;铅球出手后,经过4秒到达离地面3米的高度,经过10秒落到地面.如图建立平面直角坐标系.
米;铅球出手后,经过4秒到达离地面3米的高度,经过10秒落到地面.如图建立平面直角坐标系.
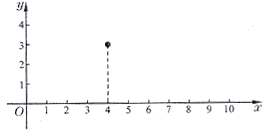
(Ⅰ)为了求这个二次函数的解析式,需要该二次函数图象上三个点的坐标.根据题意可知,该二次函数图象上三个点的坐标分别是____________________________;
(Ⅱ)求这个二次函数的解析式和自变量![]() 的取值范围.
的取值范围.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:
甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断

A.甲正确,乙错误 B.乙正确,甲错误 C.甲、乙均正确 D.甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星光厨具店购进电饭煲和电压锅两种电器进行销售其进价与售价如表
进价(元/台) | 售价(元/台) | |
电饭煲 | 200 | 250 |
电压锅 | 160 | 200 |
(1)一季度,厨具店购进这两种电器共30台,用去了5600元,并且全部售完,问厨具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度厨具店决定采购电饭煲和电压锅共50台,且电饭煲的数量不大于电压锅的![]() ,请你通过计算判断,如何进货厨具店赚钱最多?最大利润是多少?
,请你通过计算判断,如何进货厨具店赚钱最多?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
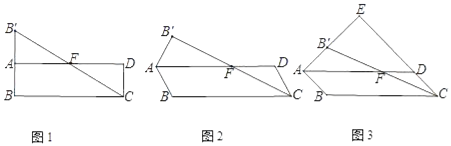
【题目】在ABCD中,点B关于AD的对称点为B′,连接AB′,CB′,CB′交AD于F点.
(1)如图1,∠ABC=90°,求证:F为CB′的中点;
(2)小宇通过观察、实验、提出猜想:如图2,在点B绕点A旋转的过程中,点F始终为CB′的中点.小宇把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:过点B′作B′G∥CD交AD于G点,只需证三角形全等;
想法2:连接BB′交AD于H点,只需证H为BB′的中点;
想法3:连接BB′,BF,只需证∠B′BC=90°.
…
请你参考上面的想法,证明F为CB′的中点.(一种方法即可)
(3)如图3,当∠ABC=135°时,AB′,CD的延长线相交于点E,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
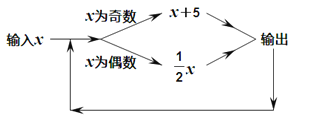
【题目】按如图所示的程序计算.若开始输入的![]() 的值为18,我们发现第1次得到的结果为9,第2次得到的结果为14,第3次得到的结果为7.……,请你探索第2019次得到的结果为_________.
的值为18,我们发现第1次得到的结果为9,第2次得到的结果为14,第3次得到的结果为7.……,请你探索第2019次得到的结果为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快递员小王下午骑摩托车从总部出发,在一条东西走向的街道上来回收送包裹.他行驶的情况记录如下(向东记为“![]() ”,向西记为“
”,向西记为“![]() ”,单位:千米):
”,单位:千米):
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)小王最后是否回到了总部?
(2)小王离总部最远是多少米?在总部的什么方向?
(3)如果小王每走![]() 米耗油
米耗油![]() 毫升,那么小王下午骑摩托车一共耗油多少毫升?
毫升,那么小王下午骑摩托车一共耗油多少毫升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,如果对角线AC和BD相交并且相等,那么我们把这样的四边形称为等角线四边形.

(1)在“平行四边形、矩形、菱形,正方形”中, 一定是等角线四边形(填写图形名称);
(2)若M、N、P、Q分别是等角线四边形ABCD四边AB、BC、CD、DA的中点,当对角线AC、BD还要满足 时,四边形MNPQ是正方形;
(3)如图2,已知△ABC中,∠ABC=90°,AB=4,BC=3,D为平面内一点.若四边形ABCD是等角线四边形,且AD=BD,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
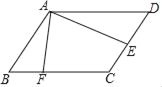
【题目】如图,在![]() ABCD中,点E为CD的中点,点F在BC上,且CF=2BF,连接AE,AF,若AF=
ABCD中,点E为CD的中点,点F在BC上,且CF=2BF,连接AE,AF,若AF=![]() ,AE=7,tan∠EAF=
,AE=7,tan∠EAF=![]() ,则线段BF的长为__________.
,则线段BF的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别是A(-3,2),B(-1,4),C(0,2).
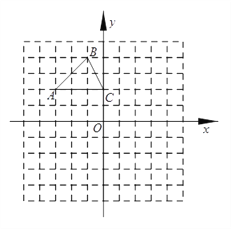
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;
(2)平移△ABC,若A的对应点A2的坐标为(-5,-2),画出平移后的△A2B2C2;
(3)若将△A2B2C2绕某一点旋转可以得到△A1B1C,请直接写出旋转中心的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com