
����Ŀ���ǹ���ߵ깺���緹�Һ͵�ѹ�����ֵ�������������������ۼ����
���ۣ�Ԫ/̨�� | �ۼۣ�Ԫ/̨�� | |
�緹�� | 200 | 250 |
��ѹ�� | 160 | 200 |
��1��һ���ȣ����ߵ깺�������ֵ�����30̨����ȥ��5600Ԫ������ȫ�����꣬�ʳ��ߵ��ڸ��������˶���Ǯ��
��2��Ϊ�������г��������ȳ��ߵ�����ɹ��緹�Һ͵�ѹ����50̨���ҵ緹�ҵ����������ڵ�ѹ����![]() ������ͨ�������жϣ���ν������ߵ�Ǯ��ࣿ��������Ƕ��٣�
������ͨ�������жϣ���ν������ߵ�Ǯ��ࣿ��������Ƕ��٣�
���𰸡���1��1400Ԫ����2���ɹ�18̨�緹�ң�32̨��ѹ��ʱ,���������2180Ԫ��
��������
ͨ�����⣬������ʾ��������Ʒ�Ľ��ۺ��ۼۣ�
��1����Ŀ�������ֵ������������ͽ������ܻ��ѣ�������һ����������x̨������һ�ֵ���������30-x��̨���ɹ����ܷ��ÿ�������ֵ�����������Ȼ���ٷֱ����ÿ�ֵ������������Ѹ��ֵ������������������
��2����Ŀ���������ֵ���������֮��Ĺ�ϵ��ͬʱ�ǵý�ϱ����е����ݣ����������е�һ�ֵ�������Ϊ n ̨��������ΪzԪ���Ӷ��г����̣��������ֵ���֮���������ϵ��ȷ��ȡֵ��Χ���Ӷ������������ֵ��
�⣺��1��ÿ���緹��������250-200=50��Ԫ����ÿ����ѹ��������200-160=40��Ԫ��
�蹺���ĵ緹��x̨�����ĵ�ѹ����30-x��̨��
������ã�200x+160��30-x��=5600
��ã�x=20
���ѹ����30-20=10��̨��
������=50��20+40��10=1400 ��Ԫ��
�𣺳��ߵ��ڸ���������1400Ԫ��
��2����ɹ��ĵ緹����n ̨����ɹ��ĵ�ѹ���У�50-n��̨
������������z=50n+40 ��50-n��=2000+10n
��n��![]() ��50-n����
��50-n����
��n��![]()
��n=18ʱ��������z�������������Ϊ2000+10��18=2180��Ԫ��
�𣺲ɹ�18̨�緹�ң�32̨��ѹ��ʱ�����ߵ�Ǯ��࣬���������2180Ԫ��
�ʴ�Ϊ����1��1400Ԫ����2���ɹ�18̨�緹�ң�32̨��ѹ��ʱ,���������2180Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
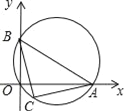
����Ŀ����ͼ����A��B�ֱ���x�ᡢy���ϣ�OA��OB������ABΪֱ����Բ����ԭ��O��C��![]() ���е㣬����AC��BC�����н��ۣ���AC=BC������OA=4��OB=2������ABC���������5������OA��OB=4�����C�������ǣ�2����2��.������ȷ�Ľ����У� ��
���е㣬����AC��BC�����н��ۣ���AC=BC������OA=4��OB=2������ABC���������5������OA��OB=4�����C�������ǣ�2����2��.������ȷ�Ľ����У� ��
A. 3�� B. 2�� C. 1�� D. 0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
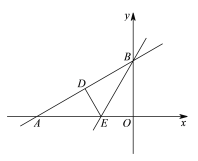
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���![]() ��x�ύ�ڵ�A����y�ύ�ڵ�B������AOB�ع���B��ֱ���۵���ʹ��O����AB���ϵĵ�D�����ۺ۽�x���ڵ�E��
��x�ύ�ڵ�A����y�ύ�ڵ�B������AOB�ع���B��ֱ���۵���ʹ��O����AB���ϵĵ�D�����ۺ۽�x���ڵ�E��
��1����ֱ��BE�Ľ���ʽ��
��2�����D�����ꣻ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶ȫ��ͬѧ�μ���ij�������������˲���ͬѧ�������ͳ����ͼ��ʾ.
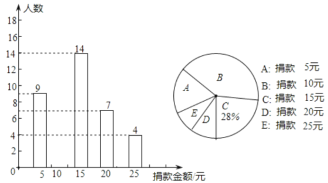
��1�����ι����ѧ�������ˣ���������ͳ��ͼ����������
��2����ֱ��д����������������λ�������������ƽ������
��3���ڰ��꼶600��ѧ���У����20Ԫ�����ϣ���20Ԫ����ѧ�������ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
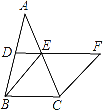
����Ŀ����ͼ������ABC�У�D��E�ֱ���AB��AC���е㣬BE=2DE���ӳ�DE����F��ʹ��EF=BE������CF��
��1����֤���ı���BCFE�����Σ�
��2����CE=4����BCF=120�㣬������BCFE�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
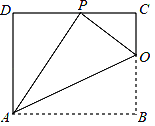
����Ŀ����ͼ����֪����ABCD��һ����AD=8��������ABCD�۵���ʹ�ö���B����CD���ϵĵ�P�����ۺ���BC���ڵ�O��
��1����֤����OCP�ס�PDA��
��2����PO��PA=1��2�����AB�ij��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
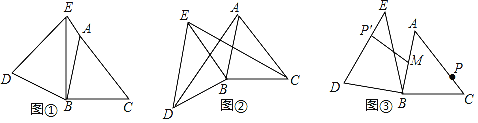
����Ŀ���������ABC�У�AB=4��BC=5����ACB=45�㣬����ABC�Ƶ�B����ʱ�뷽����ת���õ���DBE��
��1������ת����ͼ������E���߶�CA���ӳ�����ʱ������CED�Ķ������� ���ȣ�
��2������ת����ͼ��������AD��CE������ABD�����Ϊ4������CBE�������
��3����MΪ�߶�AB���е㣬��P���߶�AC��һ���㣬����ABC�Ƶ�B����ʱ�뷽����ת�����У���P�Ķ�Ӧ��P�䣬����MP�䣬��ͼ����ֱ��д���߶�MP�䳤�ȵ����ֵ����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һλ�˶�Ա��Ǧ��Ǧ������ʱ�����ĸ߶�![]() ���ף��ǹ�������ʱ��
���ף��ǹ�������ʱ��![]() ���룩�Ķ��κ�������֪Ǧ��ճ���ʱ�����ĸ߶�Ϊ
���룩�Ķ��κ�������֪Ǧ��ճ���ʱ�����ĸ߶�Ϊ![]() �ף�Ǧ����ֺ���4�뵽�������3�ĸ߶ȣ�����10���䵽���森��ͼ����ƽ��ֱ������ϵ��
�ף�Ǧ����ֺ���4�뵽�������3�ĸ߶ȣ�����10���䵽���森��ͼ����ƽ��ֱ������ϵ��
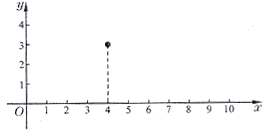
����Ϊ����������κ����Ľ���ʽ����Ҫ�ö��κ���ͼ��������������꣮���������֪���ö��κ���ͼ���������������ֱ���____________________________��
������������κ����Ľ���ʽ���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̽�Ӧ����
��1������ˮ��ɽ���ǽ�ɽ��ɽ����ijʡ2018���½�ʪ�ع���ɭ�ֹ���42��������ɭ�ֹ���ʪ�ع���4�����ʸ�ʡ2018���½�ʪ�ع���ɭ�ֹ������ٸ���
��2��ij�д��г����и߶˵ļ��õ������ۣ�ÿ�������Ľ�����2000Ԫ��������۵İ������۸õ���һ������������Ϊ20%����
�ٸõ����ı���Ƕ���Ԫ��
���������ͬһ��۵ľ������۸õ���һ������ô��õ�����Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com