
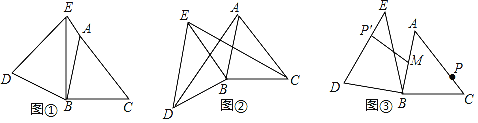
【题目】在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△DBE.
(1)当旋转成如图①,点E在线段CA的延长线上时,则∠CED的度数是 度;
(2)当旋转成如图②,连接AD、CE,若△ABD的面积为4,求△CBE的面积;
(3)点M为线段AB的中点,点P是线段AC上一动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点P′,连接MP′,如图③,直接写出线段MP′长度的最大值和最小值.
【答案】(1)90;(2)S△CBE=![]() ;(3)线段MP'的最大值为7,最小值为
;(3)线段MP'的最大值为7,最小值为![]() ﹣2.
﹣2.
【解析】试题分析:(1)根据旋转的性质可知:∠DEC=45°,再由等边对等角得∠BEC=45°,则∠CED=90°;
(2)由△ABC≌△DBE得出BA=BD,BC=BE,进而得出![]() ,证明△ABD∽△CBE,根据面积比等于相似比的平方求出△CBE的面积;
,证明△ABD∽△CBE,根据面积比等于相似比的平方求出△CBE的面积;
(3)作辅助线,当点P在F处时BP最小,则BG最小,MP'最小;当点P在点C处时,BP最大,则BH最大,MP'最大,代入计算即可得出结论.
试题解析:解:(1)由旋转得:∠DEB=∠ACB=45°,BC=BE,∴∠ACB=∠BEC=45°,∴∠CED=90°.故答案为:90;
(2)∵△ABC≌△DBE,∴BA=BD,BC=BE,∠ABC=∠DBE,∴![]() .∵∠ABD=∠CBE,∴△ABD∽△CBE,∴
.∵∠ABD=∠CBE,∴△ABD∽△CBE,∴![]() =(
=(![]() )2=
)2=![]() .∵S△ABD=4,∴S△CBE=
.∵S△ABD=4,∴S△CBE=![]() ;
;
(3)∵M是AB的中点,∴BM=![]() AB=2.如图③,过点B作BF⊥AC,F为垂足.∵△ABC为锐角三角形,∴点F在线段AC上.在Rt△BCF中,BF=BC×sin45°=
AB=2.如图③,过点B作BF⊥AC,F为垂足.∵△ABC为锐角三角形,∴点F在线段AC上.在Rt△BCF中,BF=BC×sin45°=![]() ,以B为圆心,BF为半径画圆交AB于G,BP'有最小值BG,∴MP'的最小值为MG=BG﹣BM=
,以B为圆心,BF为半径画圆交AB于G,BP'有最小值BG,∴MP'的最小值为MG=BG﹣BM=![]() ﹣2,以B为圆心,BC为半径画圆交AB的延长线于H,BP'有最大值BH.此时MP'的最大值为BM+BH=2+5=7,∴线段MP'的最大值为7,最小值为
﹣2,以B为圆心,BC为半径画圆交AB的延长线于H,BP'有最大值BH.此时MP'的最大值为BM+BH=2+5=7,∴线段MP'的最大值为7,最小值为![]() ﹣2.
﹣2.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
(1)若∠A=40°,求∠DBC的度数;
(2)若AE=6,△CBD的周长为20,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】庄子说:“一尺之椎,日取其半,万世不竭”.这句话(文字语言)表达了古人将事物无限分割的思想,用图形语言表示为图1,按此图分割的方法,可得到一个等式(符号语言):1=![]()
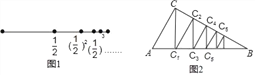
图2也是一种无限分割:在△ABC中,∠C=90°,∠B=30°,过点C作CC1⊥AB于点C1,再过点C1作C1C2⊥BC于点C2,又过点C2作C2C3⊥AB于点C3,如此无限继续下去,则可将利△ABC分割成△ACC1、△CC1C2、△C1C2C3、△C2C3C4、…、△Cn﹣2Cn﹣1Cn、….假设AC=2,这些三角形的面积和可以得到一个等式是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星光厨具店购进电饭煲和电压锅两种电器进行销售其进价与售价如表
进价(元/台) | 售价(元/台) | |
电饭煲 | 200 | 250 |
电压锅 | 160 | 200 |
(1)一季度,厨具店购进这两种电器共30台,用去了5600元,并且全部售完,问厨具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度厨具店决定采购电饭煲和电压锅共50台,且电饭煲的数量不大于电压锅的![]() ,请你通过计算判断,如何进货厨具店赚钱最多?最大利润是多少?
,请你通过计算判断,如何进货厨具店赚钱最多?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
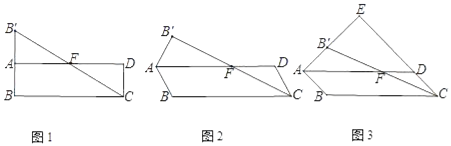
【题目】在ABCD中,点B关于AD的对称点为B′,连接AB′,CB′,CB′交AD于F点.
(1)如图1,∠ABC=90°,求证:F为CB′的中点;
(2)小宇通过观察、实验、提出猜想:如图2,在点B绕点A旋转的过程中,点F始终为CB′的中点.小宇把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:过点B′作B′G∥CD交AD于G点,只需证三角形全等;
想法2:连接BB′交AD于H点,只需证H为BB′的中点;
想法3:连接BB′,BF,只需证∠B′BC=90°.
…
请你参考上面的想法,证明F为CB′的中点.(一种方法即可)
(3)如图3,当∠ABC=135°时,AB′,CD的延长线相交于点E,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
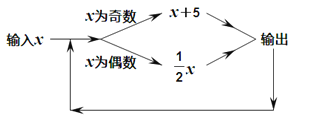
【题目】按如图所示的程序计算.若开始输入的![]() 的值为18,我们发现第1次得到的结果为9,第2次得到的结果为14,第3次得到的结果为7.……,请你探索第2019次得到的结果为_________.
的值为18,我们发现第1次得到的结果为9,第2次得到的结果为14,第3次得到的结果为7.……,请你探索第2019次得到的结果为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,如果对角线AC和BD相交并且相等,那么我们把这样的四边形称为等角线四边形.

(1)在“平行四边形、矩形、菱形,正方形”中, 一定是等角线四边形(填写图形名称);
(2)若M、N、P、Q分别是等角线四边形ABCD四边AB、BC、CD、DA的中点,当对角线AC、BD还要满足 时,四边形MNPQ是正方形;
(3)如图2,已知△ABC中,∠ABC=90°,AB=4,BC=3,D为平面内一点.若四边形ABCD是等角线四边形,且AD=BD,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E、F分别是AB、CD上的点,点G是BC的延长线上一点,且∠B=∠DCG=∠D 则下列判断错误的是( )
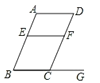
A.∠BEF=∠EFDB.∠A=∠BCFC.∠AEF=∠EBCD.∠BEF+∠EFC=180°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com