
【题目】如图1,在四边形ABCD中,如果对角线AC和BD相交并且相等,那么我们把这样的四边形称为等角线四边形.

(1)在“平行四边形、矩形、菱形,正方形”中, 一定是等角线四边形(填写图形名称);
(2)若M、N、P、Q分别是等角线四边形ABCD四边AB、BC、CD、DA的中点,当对角线AC、BD还要满足 时,四边形MNPQ是正方形;
(3)如图2,已知△ABC中,∠ABC=90°,AB=4,BC=3,D为平面内一点.若四边形ABCD是等角线四边形,且AD=BD,求四边形ABCD的面积.
【答案】(1)矩形和正方形;(2)AC⊥BD;(3)3+2![]() .
.
【解析】
(1)只有矩形和正方形的对角线相等,所以矩形和正方形是等角线四边形;
(2)当AC⊥BD时,四边形MNPQ是正方形,首先证明四边形MNPQ是菱形,再证明有一个角是直角即可;
(3)如图2中,作DE⊥AB于E.根据S四边形ABCD=S△ADE+S梯形DEBC计算,求出相关线段即可.
(1)在“平行四边形、矩形、菱形、正方形”中,
∵矩形和正方形的对角线相等,
∴矩形和正方形一定是等角线四边形,
故答案为矩形和正方形.
(2)当AC⊥BD时,四边形MNPQ是正方形.
理由:如图中,

∵M、N、P、Q分别是等角线四边形ABCD四边AB、BC、CD、DA的中点,
∴PQ=MN=![]() AC,PN=QM=
AC,PN=QM=![]() BD,PQ∥AC,MQ∥BD,
BD,PQ∥AC,MQ∥BD,
∵AC=BD,
∴MN=NP=PQ=QM,
∴四边形MNPQ是菱形,
∵∠1=∠2,∠2=∠3,∠1=90°,
∴∠3=90°,
∴四边形NMPQ是正方形.
故答案为AC⊥BD.
(3)如图2中,作DE⊥AB于E.
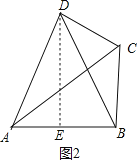
在Rt△ABC中,∵∠ABC=90°,AB=4,BC=3,
∴AC=![]() =5,
=5,
∵AD=BD,DE⊥AB,
∴AE=BE=2,
∵四边形ABCD是等角线四边形,
∴BD=AC=AD=5,
在Rt△BDE中,DE=![]() =
=![]() ,
,
∴S四边形ABCD=S△ADE+S梯形DEBC
=![]() AEDE+
AEDE+![]() (DE+BC)BE
(DE+BC)BE
=![]() ×2×
×2×![]() +
+![]() (
(![]() +3)×2
+3)×2
=3+2![]() .
.
故答案为3+2![]() .
.


科目:初中数学 来源: 题型:
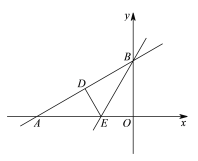
【题目】如图,在平面直角坐标系xOy中,一次函数![]() 与x轴交于点A,与y轴交于点B.将△AOB沿过点B的直线折叠,使点O落在AB边上的点D处,折痕交x轴于点E.
与x轴交于点A,与y轴交于点B.将△AOB沿过点B的直线折叠,使点O落在AB边上的点D处,折痕交x轴于点E.
(1)求直线BE的解析式;
(2)求点D的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
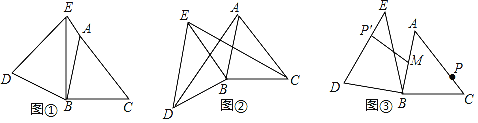
【题目】在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△DBE.
(1)当旋转成如图①,点E在线段CA的延长线上时,则∠CED的度数是 度;
(2)当旋转成如图②,连接AD、CE,若△ABD的面积为4,求△CBE的面积;
(3)点M为线段AB的中点,点P是线段AC上一动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点P′,连接MP′,如图③,直接写出线段MP′长度的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位运动员推铅球,铅球运行时离地面的高度![]() (米)是关于运行时间
(米)是关于运行时间![]() (秒)的二次函数.已知铅球刚出手时离地面的高度为
(秒)的二次函数.已知铅球刚出手时离地面的高度为![]() 米;铅球出手后,经过4秒到达离地面3米的高度,经过10秒落到地面.如图建立平面直角坐标系.
米;铅球出手后,经过4秒到达离地面3米的高度,经过10秒落到地面.如图建立平面直角坐标系.
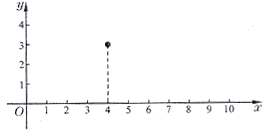
(Ⅰ)为了求这个二次函数的解析式,需要该二次函数图象上三个点的坐标.根据题意可知,该二次函数图象上三个点的坐标分别是____________________________;
(Ⅱ)求这个二次函数的解析式和自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在草莓上市的旺季,小颖和妈妈周末计划去草莓园采摘草莓.甲、乙两家草莓园生产的草莓品质相同,每千克售价均为![]() 元.甲草莓园的优惠方案是:游客进园需购买每人
元.甲草莓园的优惠方案是:游客进园需购买每人![]() 元的门票,采摘的草莓按六折收费;乙草莓园的优惠方案是:游客进园不需购买门票,采摘的草莓超过
元的门票,采摘的草莓按六折收费;乙草莓园的优惠方案是:游客进园不需购买门票,采摘的草莓超过![]() 千克后,超过部分按五折收费.请你回答下列问题:
千克后,超过部分按五折收费.请你回答下列问题:
(1)如果去乙草莓园采摘![]() 千克草莓,需支付多少元?
千克草莓,需支付多少元?
(2)如果![]() 个人去甲草莓园采摘
个人去甲草莓园采摘![]() 千克草莓,需支付多少元?
千克草莓,需支付多少元?
(3)小颖和妈妈准备采摘![]() 千克草莓送给朋友,哪家会更便宜?请说明理由.
千克草莓送给朋友,哪家会更便宜?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+5(k为常数,且k≠0)的图象与反比例函数y=-![]() 的图象交于A(-2,b),B两点.
的图象交于A(-2,b),B两点.
(1)求一次函数的表达式;
(2)若将直线AB向下平移m(m>0)个单位长度后,与反比例函数的图象有且只有一个公共点,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,BC=2AB,对角线相交于O,过C点作CE⊥BD交BD于E点,H为BC中点,连接AH交BD于G点,交EC的延长线于F点,下列5个结论:①EH=AB;②∠ABG=∠HEC;③△ABG≌△HEC;④S△GAD=S四边形GHCE;⑤CF=BD.正确的有( )个.
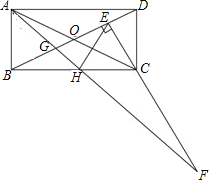
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题
(1)“绿水青山就是金山银山”,某省2018年新建湿地公园和森林公园共42个,其中森林公园比湿地公园多4个.问该省2018年新建湿地公园和森林公园各多少个?
(2)某市大市场进行高端的家用电器销售,每件电器的进价是2000元,若按标价的八折销售该电器一件,则利润率为20%.求:
①该电器的标价是多少元?
②现如果按同一标价的九折销售该电器一件,那么获得的利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B两个蔬菜市场各有蔬菜14吨,现要全部运往甲、乙两地,其中甲地需要蔬菜15吨,乙地需要蔬菜13吨,从蔬菜市场A到甲地运费50元/吨,到乙地30元/吨;从蔬菜市场B到甲地运费60元/吨,到乙地45元/吨。
(1)设从蔬菜市场A向甲地运送蔬菜x吨,请完成下表:
运往甲地(单位:吨) | 运往乙地(单位:吨) | |
蔬菜市场A | x | |
蔬菜市场B |
(2)若总运费为1300元,则从蔬菜市场A向甲地运送蔬菜多少吨?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com