
ЁОЬтФПЁПСаЗНГЬНтгІгУЬт
ЃЈ1ЃЉЁАТЬЫЎЧрЩНОЭЪЧН№ЩНвјЩНЁБЃЌФГЪЁ2018ФъаТНЈЪЊЕиЙЋдАКЭЩСжЙЋдАЙВ42ИіЃЌЦфжаЩСжЙЋдАБШЪЊЕиЙЋдАЖр4ИіЃЎЮЪИУЪЁ2018ФъаТНЈЪЊЕиЙЋдАКЭЩСжЙЋдАИїЖрЩйИіЃП
ЃЈ2ЃЉФГЪаДѓЪаГЁНјааИпЖЫЕФМвгУЕчЦїЯњЪлЃЌУПМўЕчЦїЕФНјМлЪЧ2000дЊЃЌШєАДБъМлЕФАЫелЯњЪлИУЕчЦївЛМўЃЌдђРћШѓТЪЮЊ20%ЃЎЧѓЃК
ЂйИУЕчЦїЕФБъМлЪЧЖрЩйдЊЃП
ЂкЯжШчЙћАДЭЌвЛБъМлЕФОХелЯњЪлИУЕчЦївЛМўЃЌФЧУДЛёЕУЕФРћШѓЮЊЖрЩйдЊЃП
ЁОД№АИЁПЃЈ1ЃЉЪЊЕиЙЋдА19ИіЃЌЩСжЙЋдА23ИіЃЛЃЈ2ЃЉЂйБъМлЮЊ3000дЊЃЛЂкЛёРћ700дЊ.
ЁОНтЮіЁП
ЃЈ1ЃЉЩшЪЊЕиЙЋдАxИіЃЌЩСжЙЋдАЮЊЃЈx+4ЃЉИіЃЌСаЗНГЬМЦЫуЃЌМДПЩЧѓГіД№АИЃЛ
ЃЈ2ЃЉЂйЩшБъМлЮЊmдЊЃЌИљОнЬтвтСаГіЗНГЬЃЌМДПЩЕУЕНД№АИЃЛ
ЂкРћгУБъМл![]() дМлЃЌМДПЩЕУЕНРћШѓ.
дМлЃЌМДПЩЕУЕНРћШѓ.
НтЃКЃЈ1ЃЉИљОнЬтвтЃЌЩшЪЊЕиЙЋдАxИіЃЌЩСжЙЋдАЮЊЃЈx+4ЃЉИіЃЌдђ
![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁрЪЊЕиЙЋдАга19ИіЃЌ
ЁрЩСжЙЋдАгаЃК19+4=23ЃЈИіЃЉЃЛ
ЃЈ2ЃЉЂйИљОнЬтвтЃЌЩшБъМлЮЊmдЊЃЌдђ
![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁрИУЕчЦїЕФБъМлЮЊ3000дЊЃЛ
Ђк![]() дЊЃЌ
дЊЃЌ
ЁрЛёЕУРћШѓЮЊ700дЊ.


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЧЙтГјОпЕъЙКНјЕчЗЙьвКЭЕчбЙЙјСНжжЕчЦїНјааЯњЪлЦфНјМлгыЪлМлШчБэ
НјМлЃЈдЊ/ЬЈЃЉ | ЪлМлЃЈдЊ/ЬЈЃЉ | |
ЕчЗЙьв | 200 | 250 |
ЕчбЙЙј | 160 | 200 |
ЃЈ1ЃЉвЛМОЖШЃЌГјОпЕъЙКНјетСНжжЕчЦїЙВ30ЬЈЃЌгУШЅСЫ5600дЊЃЌВЂЧвШЋВПЪлЭъЃЌЮЪГјОпЕъдкИУТђТєжазЌСЫЖрЩйЧЎЃП
ЃЈ2ЃЉЮЊСЫТњзуЪаГЁашЧѓЃЌЖўМОЖШГјОпЕъОіЖЈВЩЙКЕчЗЙьвКЭЕчбЙЙјЙВ50ЬЈЃЌЧвЕчЗЙьвЕФЪ§СПВЛДѓгкЕчбЙЙјЕФ![]() ЃЌЧыФуЭЈЙ§МЦЫуХаЖЯЃЌШчКЮНјЛѕГјОпЕъзЌЧЎзюЖрЃПзюДѓРћШѓЪЧЖрЩйЃП
ЃЌЧыФуЭЈЙ§МЦЫуХаЖЯЃЌШчКЮНјЛѕГјОпЕъзЌЧЎзюЖрЃПзюДѓРћШѓЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдкЫФБпаЮABCDжаЃЌШчЙћЖдНЧЯпACКЭBDЯрНЛВЂЧвЯрЕШЃЌФЧУДЮвУЧАбетбљЕФЫФБпаЮГЦЮЊЕШНЧЯпЫФБпаЮЃЎ

ЃЈ1ЃЉдкЁАЦНааЫФБпаЮЁЂОиаЮЁЂСтаЮЃЌе§ЗНаЮЁБжаЃЌ вЛЖЈЪЧЕШНЧЯпЫФБпаЮЃЈЬюаДЭМаЮУћГЦЃЉЃЛ
ЃЈ2ЃЉШєMЁЂNЁЂPЁЂQЗжБ№ЪЧЕШНЧЯпЫФБпаЮABCDЫФБпABЁЂBCЁЂCDЁЂDAЕФжаЕуЃЌЕБЖдНЧЯпACЁЂBDЛЙвЊТњзу ЪБЃЌЫФБпаЮMNPQЪЧе§ЗНаЮЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌвбжЊЁїABCжаЃЌЁЯABCЃН90ЁуЃЌABЃН4ЃЌBCЃН3ЃЌDЮЊЦНУцФквЛЕуЃЎШєЫФБпаЮABCDЪЧЕШНЧЯпЫФБпаЮЃЌЧвADЃНBDЃЌЧѓЫФБпаЮABCDЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() ABCDжаЃЌЕуEЮЊCDЕФжаЕуЃЌЕуFдкBCЩЯЃЌЧвCF=2BFЃЌСЌНгAEЃЌAFЃЌШєAF=
ABCDжаЃЌЕуEЮЊCDЕФжаЕуЃЌЕуFдкBCЩЯЃЌЧвCF=2BFЃЌСЌНгAEЃЌAFЃЌШєAF=![]() ЃЌAE=7ЃЌtanЁЯEAF=
ЃЌAE=7ЃЌtanЁЯEAF=![]() ЃЌдђЯпЖЮBFЕФГЄЮЊ__________ЃЎ
ЃЌдђЯпЖЮBFЕФГЄЮЊ__________ЃЎ
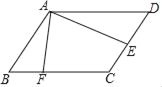
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉШчЭМЫљЪОЕФМзЁЂввСНИіЦНУцЭМаЮФмелЪВУДМИКЮЬхЃП
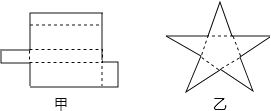
ЃЈ2ЃЉгЩЖрИіЦНУцЮЇГЩЕФМИКЮЬхНазіЖрУцЬхЃЎШєвЛИіЖрУцЬхЕФУцЪ§ЮЊfЃЌЖЅЕуИіЪ§ЮЊvЃЌРтЪ§ЮЊeЃЌЗжБ№МЦЫуЕкЃЈ1ЃЉЬтжаСНИіЖрУцЬхЕФf+vЉeЕФжЕЃПФуЗЂЯжЪВУДЙцТЩЃП
ЃЈ3ЃЉгІгУЩЯЪіЙцТЩНтОіЮЪЬтЃКвЛИіЖрУцЬхЕФЖЅЕуЪ§БШУцЪ§Дѓ8ЃЌЧвга50ЬѕРтЃЌЧѓетИіМИКЮЬхЕФУцЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDжаЃЌAB=4ЃЌBC=8ЃЌPЃЌQЗжБ№ЪЧжБЯпBCЃЌABЩЯЕФСНИіЖЏЕуЃЌAE=2ЃЌЁїAEQбиEQЗелаЮГЩЁїFEQЃЌСЌНгPFЃЌPDЃЌдђPF+PDЕФзюаЁжЕЪЧЃЈЃЉ.
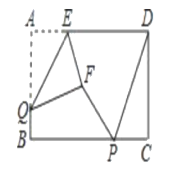
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуEЁЂFЗжБ№ЪЧABЁЂCDЩЯЕФЕуЃЌЕуGЪЧBCЕФбгГЄЯпЩЯвЛЕуЃЌЧвЁЯB=ЁЯDCG=ЁЯD дђЯТСаХаЖЯДэЮѓЕФЪЧЃЈ ЃЉ
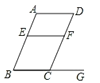
A.ЁЯBEF=ЁЯEFDB.ЁЯA=ЁЯBCFC.ЁЯAEF=ЁЯEBCD.ЁЯBEF+ЁЯEFC=180Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ8ЗжЃЉШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЁїABCЕФШ§ИіЖЅЕуЕФзјБъЗжБ№ЪЧAЃЈ-3,2ЃЉЃЌB(-1,4ЃЉЃЌCЃЈ0ЃЌ2ЃЉЃЎ
ЃЈ1ЃЉНЋЁїABCвдЕуCЮЊа§зЊжааФа§зЊ180ЁуЃЌЛГіа§зЊКѓЖдгІЕФЁїA1B1CЃЛ
ЃЈ2ЃЉЦНвЦЁїABCЃЌШєAЕФЖдгІЕуA2ЕФзјБъЮЊ(-5,-2ЃЉЃЌЛГіЦНвЦКѓЕФЁїA2B2C2ЃЛ
ЃЈ3ЃЉШєНЋЁїA2B2C2ШЦФГвЛЕуа§зЊПЩвдЕУЕНЁїA1B1CЃЌЧыжБНгаДГіа§зЊжааФЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
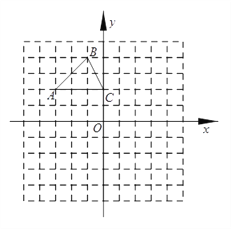
ЁОЬтФПЁПШчЭМЃЌRtЁїABCжаЃЌЁЯC=90ЁуЃЌЁЯA=30ЁуЃЌBC=2ЃЌCDЪЧаББпABЩЯЕФИпЃЌЕуEЮЊБпACЩЯвЛЕуЃЈЕуEВЛгыЕуAЁЂCжиКЯЃЉЃЌСЊНсDEЃЌзїCFЁЭDEЃЌCFгыБпABЁЂЯпЖЮDEЗжБ№НЛгкЕуFЁЂGЃЛ
ЃЈ1ЃЉЧѓЯпЖЮCDЁЂADЕФГЄЃЛ
ЃЈ2ЃЉЩшCE=xЃЌDF=yЃЌЧѓyЙигкxЕФКЏЪ§НтЮіЪНЃЌВЂаДГіЫќЕФЖЈвхгђЃЛ
ЃЈ3ЃЉСЊНсEFЃЌЕБЁїEFGгыЁїCDGЯрЫЦЪБЃЌЧѓЯпЖЮCEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com