练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，矩形ABCD中，BC=2AB，对角线相交于O，过C点作CE⊥BD交BD于E点，H为BC中点，连接AH交BD于G点，交EC的延长线于F点，下列5个结论：①EH=AB；②∠ABG=∠HEC；③△ABG≌△HEC；④S△GAD=S四边形GHCE；⑤CF=BD．正确的有（　　）个．

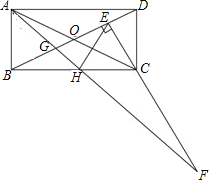
    A. 2 B. 3 C. 4 D. 5

    【答案】B

    【解析】试题解析：由图可知， ，因为 ,所以 ,故①正确；

    因为 ,所以 ,由于 ， ，所以 ,则 ,故②正确；

    在△ABG与△HEC中， ，从而两三角形不全等，故③错误；

    过点A作AM⊥BG于点M，由图可知 ，而 ，即

    ，则 ，故④错误；

    因为 ， ， ，所以

    ，又因为 ，所以 ，则

    ，故⑤正确.

    综上所述，正确的结论有3个，故选B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】庄子说：“一尺之椎，日取其半，万世不竭”．这句话（文字语言）表达了古人将事物无限分割的思想，用图形语言表示为图1，按此图分割的方法，可得到一个等式（符号语言）：1=

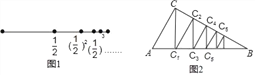
    图2也是一种无限分割：在△ABC中，∠C=90°，∠B=30°，过点C作CC1⊥AB于点C1，再过点C1作C1C2⊥BC于点C2，又过点C2作C2C3⊥AB于点C3，如此无限继续下去，则可将利△ABC分割成△ACC1、△CC1C2、△C1C2C3、△C2C3C4、…、△Cn﹣2Cn﹣1Cn、…．假设AC=2，这些三角形的面积和可以得到一个等式是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

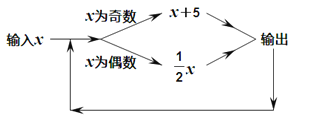
    【题目】按如图所示的程序计算.若开始输入的的值为18，我们发现第1次得到的结果为9，第2次得到的结果为14，第3次得到的结果为7.……，请你探索第2019次得到的结果为_________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在四边形ABCD中，如果对角线AC和BD相交并且相等，那么我们把这样的四边形称为等角线四边形．

    （1）在“平行四边形、矩形、菱形，正方形”中， 一定是等角线四边形（填写图形名称）；

    （2）若M、N、P、Q分别是等角线四边形ABCD四边AB、BC、CD、DA的中点，当对角线AC、BD还要满足 时，四边形MNPQ是正方形；

    （3）如图2，已知△ABC中，∠ABC＝90°，AB＝4，BC＝3，D为平面内一点．若四边形ABCD是等角线四边形，且AD＝BD，求四边形ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】实践与探索：将连续的奇数 1，3，5，7…排列成如下的数表，用十字框框出 5 个数(如图)

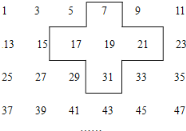
    (1)若将十字框上下左右平移，但一定要框住数列中的 5 个数，若设中间的数为 a，用 a 的代数式表示十字框框住的 5 个数字之和；

    (2)十字框框住的 5 个数之和能等于 285 吗？若能，分别写出十字框框住的 5 个数；若不能，请说明理由；

    (3)十字框框住的 5 个数之和能等于 365 吗？若能，分别写出十字框框住的 5 个数；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

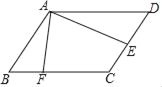
    【题目】如图，在ABCD中，点E为CD的中点，点F在BC上，且CF=2BF，连接AE，AF，若AF=，AE=7，tan∠EAF=，则线段BF的长为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】回答下列问题：

    （1）如图所示的甲、乙两个平面图形能折什么几何体？

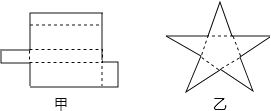
    （2）由多个平面围成的几何体叫做多面体．若一个多面体的面数为f，顶点个数为v，棱数为e，分别计算第（1）题中两个多面体的f+v﹣e的值？你发现什么规律？

    （3）应用上述规律解决问题：一个多面体的顶点数比面数大8，且有50条棱，求这个几何体的面数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点E、F分别是AB、CD上的点，点G是BC的延长线上一点，且∠B=∠DCG=∠D 则下列判断错误的是（ ）

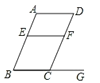
    A.∠BEF=∠EFDB.∠A=∠BCFC.∠AEF=∠EBCD.∠BEF+∠EFC=180°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在互联网技术的影响下，幸福新村的村民小刘在网上销售苹果，原计划每天卖100千克，但实际每天的销量与计划销量相比有出入，如表是某周的销售情况（超额记为正，不足记为负.单位：千克）：

    星期

    一

    二

    三

    四

    五

    六

    日

    与计划量的差值

    （1）根据表中的数据可知前三天共卖出___________千克；

    （2）根据记录的数据可知销售量最多的一天比销售量最少的一天多销售多少千克？

    （3）若每千克按5元出售，每千克苹果的运费为1元，那么小刘本周一共收入多少元？

    查看答案和解析>>

    同步练习册答案