
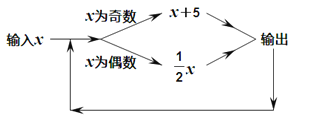
【题目】按如图所示的程序计算.若开始输入的![]() 的值为18,我们发现第1次得到的结果为9,第2次得到的结果为14,第3次得到的结果为7.……,请你探索第2019次得到的结果为_________.
的值为18,我们发现第1次得到的结果为9,第2次得到的结果为14,第3次得到的结果为7.……,请你探索第2019次得到的结果为_________.
【答案】2
【解析】
把x=18代入程序中计算,以此类推得到一般性规律,求出第2019次的得到的结果即可.
解:第1次得到的结果为18×![]() =9,
=9,
第2次得到的结果为9+5=14,
第3次得到的结果为14×![]() =7,
=7,
第4次得到的结果为7+5=12,
第5次得到的结果为12×![]() =6,
=6,
第6次得到的结果为6×![]() =3,
=3,
第7次得到的结果为3+5=8,
第8次得到的结果为8×![]() =4,
=4,
第9次得到的结果为4×![]() =2,
=2,
第10次得到的结果为2×![]() =1,
=1,
第11次的到的结果为1+5=6,
第12次得到的结果为6×![]() =3,
=3,
……
∴从第5次开始,以6,3,8,4,2,1这6个数为周期循环,
∵(2019-4)÷6=335…5,
∴第2019次得到的结果为2,
故答案为:2.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】.计算:
(1)23﹣17﹣(﹣7)+(﹣16)
(2)![]()
(3) -1.2×4÷(-![]() )+
)+![]() ÷(--2an =1
÷(--2an =1![]() ) ×(-
) ×(-![]() )
)
(4)﹣14﹣8÷(﹣2)3+22×(﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
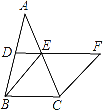
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
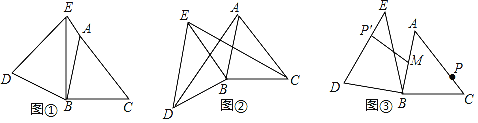
【题目】在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△DBE.
(1)当旋转成如图①,点E在线段CA的延长线上时,则∠CED的度数是 度;
(2)当旋转成如图②,连接AD、CE,若△ABD的面积为4,求△CBE的面积;
(3)点M为线段AB的中点,点P是线段AC上一动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点P′,连接MP′,如图③,直接写出线段MP′长度的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】世界杯比赛中,根据场上攻守形势,守门员会在门前来回跑动,如果以球门线为基准,向前跑记作正数,返回则记作负数,一段时间内,某守门员的跑动情况记录如下(单位:m):+10,﹣2,+5,﹣6,+12,﹣9,+4,﹣14.(假定开始计时时,守门员正好在球门线上)
(1)守门员最后是否回到球门线上?
(2)守门员离开球门线的最远距离达多少米?
(3)如果守门员离开球门线的距离超过10米(不包括10米),则对方球员挑射极可能造成破门.请问在这一时间段内,对方球员有几次挑射破门的机会?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位运动员推铅球,铅球运行时离地面的高度![]() (米)是关于运行时间
(米)是关于运行时间![]() (秒)的二次函数.已知铅球刚出手时离地面的高度为
(秒)的二次函数.已知铅球刚出手时离地面的高度为![]() 米;铅球出手后,经过4秒到达离地面3米的高度,经过10秒落到地面.如图建立平面直角坐标系.
米;铅球出手后,经过4秒到达离地面3米的高度,经过10秒落到地面.如图建立平面直角坐标系.
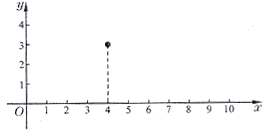
(Ⅰ)为了求这个二次函数的解析式,需要该二次函数图象上三个点的坐标.根据题意可知,该二次函数图象上三个点的坐标分别是____________________________;
(Ⅱ)求这个二次函数的解析式和自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在草莓上市的旺季,小颖和妈妈周末计划去草莓园采摘草莓.甲、乙两家草莓园生产的草莓品质相同,每千克售价均为![]() 元.甲草莓园的优惠方案是:游客进园需购买每人
元.甲草莓园的优惠方案是:游客进园需购买每人![]() 元的门票,采摘的草莓按六折收费;乙草莓园的优惠方案是:游客进园不需购买门票,采摘的草莓超过
元的门票,采摘的草莓按六折收费;乙草莓园的优惠方案是:游客进园不需购买门票,采摘的草莓超过![]() 千克后,超过部分按五折收费.请你回答下列问题:
千克后,超过部分按五折收费.请你回答下列问题:
(1)如果去乙草莓园采摘![]() 千克草莓,需支付多少元?
千克草莓,需支付多少元?
(2)如果![]() 个人去甲草莓园采摘
个人去甲草莓园采摘![]() 千克草莓,需支付多少元?
千克草莓,需支付多少元?
(3)小颖和妈妈准备采摘![]() 千克草莓送给朋友,哪家会更便宜?请说明理由.
千克草莓送给朋友,哪家会更便宜?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,BC=2AB,对角线相交于O,过C点作CE⊥BD交BD于E点,H为BC中点,连接AH交BD于G点,交EC的延长线于F点,下列5个结论:①EH=AB;②∠ABG=∠HEC;③△ABG≌△HEC;④S△GAD=S四边形GHCE;⑤CF=BD.正确的有( )个.
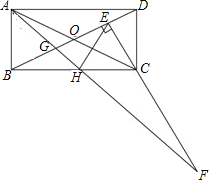
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:如图1,圆的概念:在平面内,线段PA绕它固定的一个端点P旋转一周,另一个端点A所形成的图形叫做圆.就是说,到某个定点等于定长的所有点在同一个圆上.圆心在P(a,b),半径为r的圆的方程可以写为:(x-a)2+(y-b)2=r2.如:圆心在P(2,-1),半径为5的圆的方程为:(x-2)2+(y+1)2=25.
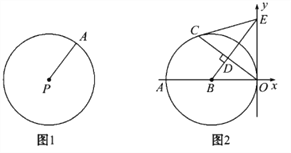
(1)填空: ①以A(3,0)为圆心,1为半径的圆的方程为:________; ②以B(-1,-2)为圆心, ![]() 为半径的圆的方程为:________;
为半径的圆的方程为:________;
(2)根据以上材料解决以下问题:
如图2,以B(-6,0)为圆心的圆与y轴相切于原点,C是☉B上一点,连接OC,作BD⊥OC垂足为D,延长BD交y轴于点E,已知sin∠AOC=![]() .
.
①连接EC,证明EC是☉B的切线;
②在BE上是否存在一点P,使PB=PC=PE=PO,若存在,求P点坐标,并写出以P为圆心,以PB为半径的☉P的方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com