
【题目】阅读下面材料:如图1,圆的概念:在平面内,线段PA绕它固定的一个端点P旋转一周,另一个端点A所形成的图形叫做圆.就是说,到某个定点等于定长的所有点在同一个圆上.圆心在P(a,b),半径为r的圆的方程可以写为:(x-a)2+(y-b)2=r2.如:圆心在P(2,-1),半径为5的圆的方程为:(x-2)2+(y+1)2=25.
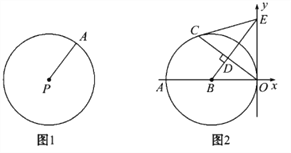
(1)填空: ①以A(3,0)为圆心,1为半径的圆的方程为:________; ②以B(-1,-2)为圆心, ![]() 为半径的圆的方程为:________;
为半径的圆的方程为:________;
(2)根据以上材料解决以下问题:
如图2,以B(-6,0)为圆心的圆与y轴相切于原点,C是☉B上一点,连接OC,作BD⊥OC垂足为D,延长BD交y轴于点E,已知sin∠AOC=![]() .
.
①连接EC,证明EC是☉B的切线;
②在BE上是否存在一点P,使PB=PC=PE=PO,若存在,求P点坐标,并写出以P为圆心,以PB为半径的☉P的方程;若不存在,说明理由.
【答案】(1)①方程为:(x-3)2+y2=1;②方程为:(x+1)2+(y+2)2=3.(2)①证明见解析;②存在,证明见解析.
【解析】(1)根据阅读材料中的定义求解;
(2)①根据垂径定理由BD⊥OC得到CD=OD,则BE垂直平分OC,再根据线段垂直平分线的性质得EO=EC,则∠EOC=∠ECO,
加上∠BOC=∠BCO,易得∠BOE=∠BCE=90°,然后根据切线的判定定理得到EC是⊙B的切线;
②由∠BOE=∠BCE=90°,根据圆周角定理得点C和点O偶在以BE为直径的圆上,即当P点为BE的中点时,满足PB=PC=PE=PO,利用同角的余角相等得∠BOE=∠AOC,则sin∠BOE=sin∠AOC=![]() ,在Rt△BOE中,利用正弦的定3义计算出BE=10,利用勾股定理计算出OE=8,则E点坐标为(0,8),于是得到线段AB的中点P的坐标为(﹣3,4),PB=5,然后写出以P(﹣3,4)为圆心,以5为半径的⊙P的方程.
,在Rt△BOE中,利用正弦的定3义计算出BE=10,利用勾股定理计算出OE=8,则E点坐标为(0,8),于是得到线段AB的中点P的坐标为(﹣3,4),PB=5,然后写出以P(﹣3,4)为圆心,以5为半径的⊙P的方程.
解:①以A(3,0)为圆心,1为半径的圆的方程为(x﹣3)2+y2=1;
②以B(﹣1,﹣2)为圆心, ![]() 为半径的圆的方程为(x+1)2+(y+2)2=3;
为半径的圆的方程为(x+1)2+(y+2)2=3;
故答案为(x﹣3)2+y2=1;(x+1)2+(y+2)2=3;
(2)①连接BC.
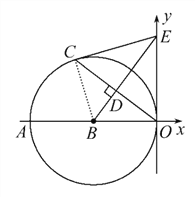
∵OB=BC,BD⊥OC,∴∠OBD=∠CBD.
又∵BE=BE,
∴△BOE≌△BCE,
∴∠BCE=∠BOE.
∵AO⊥OE,∴∠BCE=90°.
∴EC是☉B的切线.
②存在.
取BE的中点P,连接PC,PO.
∵△BCE和△BOE是直角三角形,
∴PC=![]() BE,PO=
BE,PO=![]() BE,
BE,
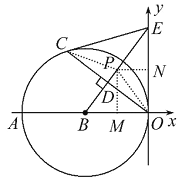
∴PC=PB=PO=PE.
过P作PM⊥x轴于M,PN⊥y轴于N.
∵P是BE中点,∴OM=![]() OB,ON=
OB,ON=![]() OE.
OE.
∵∠AOC+∠EOC=90°,∠BEO+∠EOC=90°,
∴∠AOC=∠BEO.
∵sin∠AOC=![]() ,∴sin∠BEO=
,∴sin∠BEO=![]() .
.
∴![]() =
=![]() ,即
,即![]() =
=![]() ,∴BE=10.
,∴BE=10.
由勾股定理:OE=![]() =8,
=8,
P(-3,4),PB=![]() =5.
=5.
∴☉P的方程为(x+3)2+(y-4)2=25.
“点睛”本题了圆的综合题:熟练掌握垂径定理、切线的判定定理、圆周角定理和等腰三角形的性质;阅读理解能力也是本题考查的重点;会运用锐角三角函数的定义和勾股定理进行几何计算.


科目:初中数学 来源: 题型:
【题目】某商家预测一种应季衬衫能畅销市场,就用13 200元购进了一批这种衬衫,面市后果然供不应求,商家又用28 800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完利润率不低于25%(不考虑其他因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】毕达哥拉斯学派对”数”与”形”的巧妙结合作了如下研究:
名称及图形 | 三角形数 | 正方形数 | 五边形数 | 六边形数 |
|
|
|
| |
第一层几何点数 | 1 | 1 | 1 | 1 |
第二层几何点数 | 2 | 3 | 4 | 5 |
第三层几何点数 | 3 | 5 | 7 | 9 |
… | … | … | … | … |
第六层几何点数 | ||||
… | … | … | … | … |
第n层几何点数 |
请写出第六层各个图形的几何点数,并归纳出第n层各个图形的几何点数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过A(﹣3.0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.
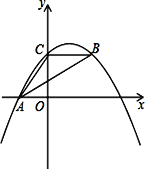
(1)求抛物线的解析式a,b,c;
(2)线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;
(3)抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在求出点M坐标;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线y=x2+bx+c与x轴交于A、B两点(点A在点B左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.
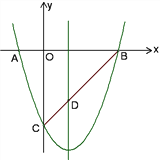
(1)求抛物线的函数表达式;
(2)求直线BC的函数表达式;
(3)点E为y轴上一动点,CE的垂直平分线交CE于点F,交抛物线于P、Q两点,且点P在第三象限.
①当线段PQ ![]() 时,求tan∠CED的值;
时,求tan∠CED的值;
②当以C、D、E为顶点的三角形是直角三角形时,请直接写出点P的坐标.
(参考公式:抛物线![]() 的顶点坐标是
的顶点坐标是 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com