
【题目】下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. 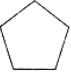 B.
B. 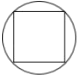 C.
C. 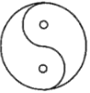 D.
D. 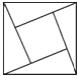
【答案】B
【解析】
中心对称图形绕某一点旋转180°后的图形与原来的图形重合,轴对称图形被一条直线分割成的两部分沿着对称轴折叠时,互相重合,据此逐一判断出既是轴对称图形又是中心对称图形的是哪个即可.
∵A中的图形旋转180后不能与原图形重合,
∴A中的图形不是中心对称图形,
∴选项A不正确;
∵B中的图形旋转180后能与原图形重合,
∴B中的图形是中心对称图形,
∴B中的图形既是轴对称图形,又是中心对称图形,
∴选项B正确;
∵C中的图形旋转180后能与原图形重合,
∴C中的图形是中心对称图形,但它不是轴对称图形,
∴选项C不正确;
∵D中的图形旋转180后能与原图形重合,
∴D中的图形是中心对称图形,但它不是轴对称图形,
∴选项D不正确。
故选:B.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
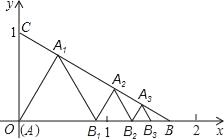
【题目】如图所示,已知直线![]() 与x、y轴交于B、C两点,A(0,0),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…则第n个等边三角形的边长等于( )
与x、y轴交于B、C两点,A(0,0),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…则第n个等边三角形的边长等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
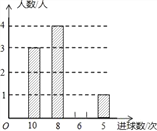
【题目】某校九年级学生在一节体育课中,选一组学生进行投篮比赛,每人投10次,汇总投进球数的情况进行统计分析,绘制了如下不完整的统计表和统计图.
次数 | 10 | 8 | 6 | 5 |
人数 | 3 | a | 2 | 1 |
(1)表中a= ;
(2)请将条形统计图补充完整;
(3)从小组成员中选一名学生参加校动会投篮比赛,投进10球的成员被选中的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
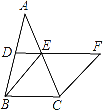
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”黄金周期间,淮安动物园在7天假期中每天接待的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数),把9月30日的游客人数记为a万人.
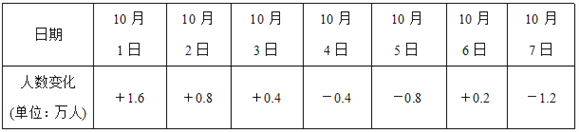
(1)请用含a的代数式表示10月2日的游客人数;
(2)请判断七天内游客人数最多的是哪天,有多少人?
(3)若9月30日的游客人数为2万人,门票每人10元,问黄金周期间淮安动物园门票收入是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
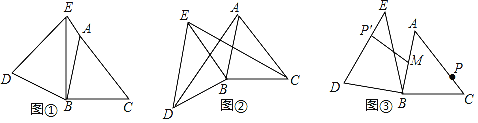
【题目】在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△DBE.
(1)当旋转成如图①,点E在线段CA的延长线上时,则∠CED的度数是 度;
(2)当旋转成如图②,连接AD、CE,若△ABD的面积为4,求△CBE的面积;
(3)点M为线段AB的中点,点P是线段AC上一动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点P′,连接MP′,如图③,直接写出线段MP′长度的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】世界杯比赛中,根据场上攻守形势,守门员会在门前来回跑动,如果以球门线为基准,向前跑记作正数,返回则记作负数,一段时间内,某守门员的跑动情况记录如下(单位:m):+10,﹣2,+5,﹣6,+12,﹣9,+4,﹣14.(假定开始计时时,守门员正好在球门线上)
(1)守门员最后是否回到球门线上?
(2)守门员离开球门线的最远距离达多少米?
(3)如果守门员离开球门线的距离超过10米(不包括10米),则对方球员挑射极可能造成破门.请问在这一时间段内,对方球员有几次挑射破门的机会?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在草莓上市的旺季,小颖和妈妈周末计划去草莓园采摘草莓.甲、乙两家草莓园生产的草莓品质相同,每千克售价均为![]() 元.甲草莓园的优惠方案是:游客进园需购买每人
元.甲草莓园的优惠方案是:游客进园需购买每人![]() 元的门票,采摘的草莓按六折收费;乙草莓园的优惠方案是:游客进园不需购买门票,采摘的草莓超过
元的门票,采摘的草莓按六折收费;乙草莓园的优惠方案是:游客进园不需购买门票,采摘的草莓超过![]() 千克后,超过部分按五折收费.请你回答下列问题:
千克后,超过部分按五折收费.请你回答下列问题:
(1)如果去乙草莓园采摘![]() 千克草莓,需支付多少元?
千克草莓,需支付多少元?
(2)如果![]() 个人去甲草莓园采摘
个人去甲草莓园采摘![]() 千克草莓,需支付多少元?
千克草莓,需支付多少元?
(3)小颖和妈妈准备采摘![]() 千克草莓送给朋友,哪家会更便宜?请说明理由.
千克草莓送给朋友,哪家会更便宜?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com