
【题目】如图,点A、B分别在x轴、y轴上(OA>OB),以AB为直径的圆经过原点O,C是![]() 的中点,连结AC,BC.下列结论:①AC=BC;②若OA=4,OB=2,则△ABC的面积等于5;③若OA﹣OB=4,则点C的坐标是(2,﹣2).其中正确的结论有( )
的中点,连结AC,BC.下列结论:①AC=BC;②若OA=4,OB=2,则△ABC的面积等于5;③若OA﹣OB=4,则点C的坐标是(2,﹣2).其中正确的结论有( )
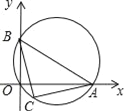
A. 3个 B. 2个 C. 1个 D. 0个
【答案】A
【解析】①∵C是![]() 的中点,∴
的中点,∴![]() ,∴AC=BC,∴①正确;
,∴AC=BC,∴①正确;
②在Rt△AOB中,OA=4,OB=2,由勾股定理得AB==2![]() ,在Rt△ABC中,AC=BC=
,在Rt△ABC中,AC=BC=![]() AB=
AB=![]() ,∴△ABC的面积=
,∴△ABC的面积=![]() ×AC×BC=
×AC×BC=![]() =5,∴②正确;
=5,∴②正确;
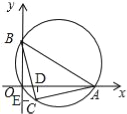
③如图,过点C作CD⊥OA,DE⊥OB,∴∠BEC=∠ADC=90°,过点C作CD⊥OA,DE⊥OB,∴∠BEC=∠ADC=90°,在△BCE和△ACD中∠BEC=∠ADC,∠CBE=∠CAD,BC=AC,∴△BCE≌△ACD,∴AD=BE,CE=CD,∵∠DOE=∠OEC=∠ODC=90°,∴四边形ODCE是矩形,∵CE=CD,∴矩形ODCE是正方形,∴OD=OD=CD=CE,∵AD=OA﹣OD,BE=OB+BE=OB+OD,∵AD=BE,∴OA﹣OD=OB+OD,∵OA﹣OB=4,∴OD=2,∴CD=CE=2,∴C(2,﹣2)∴③正确,故选A.


科目:初中数学 来源: 题型:
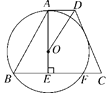
【题目】如图,梯形ABCD中,AD∥BC,AE⊥BC于点E,∠ADC的平分线交AE于点O,以点O为圆心,OA为半径的圆经过点B,交BC于另一点F.
(1)求证:CD与⊙O相切;
(2)若BF=24,OE=5,求tan∠ABC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与x轴、y轴分别交于A, B两点,将△AOB沿直线AB翻折,使点O落在点C处, 点P,Q分别在AB , AC上,当PC+PQ取最小值时,直线OP的解析式为( )
与x轴、y轴分别交于A, B两点,将△AOB沿直线AB翻折,使点O落在点C处, 点P,Q分别在AB , AC上,当PC+PQ取最小值时,直线OP的解析式为( )
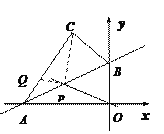
A. y=- ![]() B. y=-
B. y=- ![]() C. y=-
C. y=- ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
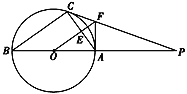
【题目】如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连结AF.
(1)判断AF与⊙O的位置关系并说明理由;
(2)若AC=24,AF=15,求sinB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 一个游戏中奖的概率是![]() ,则做100次这样的游戏一定会中奖
,则做100次这样的游戏一定会中奖
B. 为了了解全国中学生的心理健康状况,应采用普查的方式
C. 一组数据0,1,2,1,1的众数和中位数都是1
D. 若甲组数据的方差为![]() ,乙组数据的方差为
,乙组数据的方差为![]() ,则乙组数据比甲组数据稳定
,则乙组数据比甲组数据稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
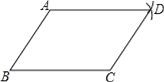
【题目】嘉琪同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图所示的□ABCD,并写出了如下尚不完整的已知和求证.
已知:如图,在四边形ABCD中,BC=AD,AB= .
求证:四边形ABCD是 四边形.
(1)补全已知和求证(在方框中填空);
(2)嘉琪同学想利用三角形全等,依据“两组对边分别平行的四边形是平行四边形”来证明.请你按她的想法完成证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
(1)若∠A=40°,求∠DBC的度数;
(2)若AE=6,△CBD的周长为20,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:
甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断

A.甲正确,乙错误 B.乙正确,甲错误 C.甲、乙均正确 D.甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星光厨具店购进电饭煲和电压锅两种电器进行销售其进价与售价如表
进价(元/台) | 售价(元/台) | |
电饭煲 | 200 | 250 |
电压锅 | 160 | 200 |
(1)一季度,厨具店购进这两种电器共30台,用去了5600元,并且全部售完,问厨具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度厨具店决定采购电饭煲和电压锅共50台,且电饭煲的数量不大于电压锅的![]() ,请你通过计算判断,如何进货厨具店赚钱最多?最大利润是多少?
,请你通过计算判断,如何进货厨具店赚钱最多?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com