
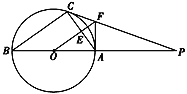
【题目】如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连结AF.
(1)判断AF与⊙O的位置关系并说明理由;
(2)若AC=24,AF=15,求sinB.
【答案】(1) AF与⊙O相切 理由见解析;(2)![]()
【解析】试题分析:(1)连接OC,先证∠OCF=90°,再证明△OAF≌△OCF,得出∠OAF=∠OCF=90°即可;
(2)先求出AE、EF,再证明△OAE∽△AFE,得出比例式![]() ,可求出半径,进而求出直径,由三角函数的定义即可得出结论.
,可求出半径,进而求出直径,由三角函数的定义即可得出结论.
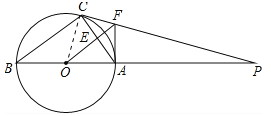
试题解析:解:(1)AF与⊙O相切.理由如下:
连接OC.如图所示.∵PC是⊙O的切线,∴OC⊥PC,∴∠OCF=90°.∵OF∥BC,∴∠B=∠AOF,∠OCB=∠COF.∵OB=OC,∴∠B=∠OCB,∴∠AOF=∠COF.在△OAF和△OCF中,∵OA=OC,∠AOF=∠COF,OF=OF,∴△OAF≌△OCF(SAS),∴∠OAF=∠OCF=90°,∴AF与⊙O相切;
(2)∵△OAF≌△OCF,∴∠OAE=∠COE,∴OE⊥AC,AE=![]() AC=12,∴EF=
AC=12,∴EF=![]() .∵∠OAF=90°,∴△OAE∽△AFE,∴
.∵∠OAF=90°,∴△OAE∽△AFE,∴![]() ,即
,即![]() ,∴OA=20,∴AB=40,sinB=
,∴OA=20,∴AB=40,sinB=![]() .
.


科目:初中数学 来源: 题型:
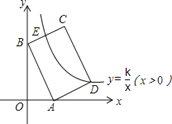
【题目】(10分)如图,在平面直角坐标系中,反比例函数![]() 的图象和矩形ABCD在第二象限,AD平行于x轴,且AB=2,AD=4,点C的坐标为(﹣2,4).
的图象和矩形ABCD在第二象限,AD平行于x轴,且AB=2,AD=4,点C的坐标为(﹣2,4).
(1)直接写出A、B、D三点的坐标;
(2)若将矩形只向下平移,矩形的两个顶点恰好同时落在反比例函数的图象上,求反比例函数的解析式和此时直线AC的解析式y=mx+n.并直接写出满足![]() 的x取值范围.
的x取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
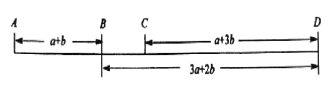
【题目】己知![]() 四个车站的位置如图所示.
四个车站的位置如图所示.
(1)求![]() 两站之间的距离;(用含
两站之间的距离;(用含![]() 的代数式表示)
的代数式表示)
(2)一辆汽车从![]() 站出发,每小时行驶60千米,经过
站出发,每小时行驶60千米,经过![]() 站到达C站(在
站到达C站(在![]() 站没有停留).所用时间为1.5小时.汽车在
站没有停留).所用时间为1.5小时.汽车在![]() 站短暂停留后,继续以相同速度行驶,再行驶2小时到达
站短暂停留后,继续以相同速度行驶,再行驶2小时到达![]() 站,求
站,求![]() 的值以及汽车从
的值以及汽车从![]() 站行驶到
站行驶到![]() 站一共用了多少小时?
站一共用了多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0),B(0,6)分别在x轴,y轴上,反比例函数y=![]() (x>0)的图象经过点D,且与边BC交于点E,则点E的坐标为__.
(x>0)的图象经过点D,且与边BC交于点E,则点E的坐标为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗,某食品厂为了解市民对去年销售量较好的肉馅粽、豆沙粽、红枣粽、蛋黄馅粽(以下分别用A,B,C,D表示这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查结果绘制成如下两幅统计图.
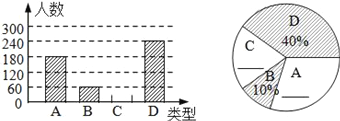
请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?将不完整的条形图和扇形图补充完整;
(2)若居民区有8000人,请估计爱吃C ,D粽的总人数;
(3)若有外型完全相同的A,B,C,D粽各一个煮熟后,小王吃了两个,用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:圆是最完美的图形,它具有一些特殊的性质:同弧或等弧所对的圆周角相等,一条弧所对的圆周角等于这条弧所对的圆心角的一半……先构造“辅助圆”,再利用圆的性质将问题进行转化,往往能化隐为显、化难为易。
解决问题:如图,点A与点B的坐标分别是(1,0),(5,0),点P是该直角坐标系内的一个动点.
(1)使∠APB=30°的点P有_______个;
(2)若点P在y轴正半轴上,且∠APB=30°,求满足条件的点P的坐标;
(3)设sin∠APB=m,若点P在y轴上移动时, 满足条件的点P有4个,求m的取值范围.
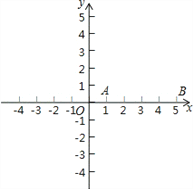
查看答案和解析>>
科目:初中数学 来源: 题型:
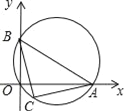
【题目】如图,点A、B分别在x轴、y轴上(OA>OB),以AB为直径的圆经过原点O,C是![]() 的中点,连结AC,BC.下列结论:①AC=BC;②若OA=4,OB=2,则△ABC的面积等于5;③若OA﹣OB=4,则点C的坐标是(2,﹣2).其中正确的结论有( )
的中点,连结AC,BC.下列结论:①AC=BC;②若OA=4,OB=2,则△ABC的面积等于5;③若OA﹣OB=4,则点C的坐标是(2,﹣2).其中正确的结论有( )
A. 3个 B. 2个 C. 1个 D. 0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了锻炼身体,强健体魄,小明和小强约定每天在两家之间往返长跑20分钟. 两家正好在同一直线道路边上,某天小明和小强从各自的家门口同时出发,沿两家之间的直线道路按各自的速度匀速往返跑步,已知小明的速度大于小强的速度. 在跑步的过程中,小明和小强两人之间的距离y(米)与他们出发的时间x(分钟)之间的关系如图所示,在他们3次相遇中,离小明家最近那次相遇时距小明家____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级全体同学参加了某项捐款活动,随机抽查了部分同学捐款的情况统计如图所示.
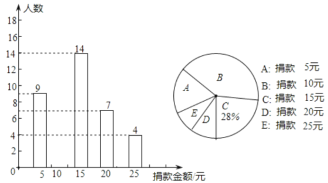
(1)本次共抽查学生多少人?并将条形统计图补充完整;
(2)请直接写出捐款金额的众数和中位数,并计算捐款的平均数;
(3)在八年级600名学生中,捐款20元及以上(含20元)的学生估计有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com