
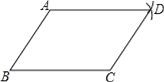
【题目】嘉琪同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图所示的□ABCD,并写出了如下尚不完整的已知和求证.
已知:如图,在四边形ABCD中,BC=AD,AB= .
求证:四边形ABCD是 四边形.
(1)补全已知和求证(在方框中填空);
(2)嘉琪同学想利用三角形全等,依据“两组对边分别平行的四边形是平行四边形”来证明.请你按她的想法完成证明过程.
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=120°,点A绕点O顺时针旋转后的对应点A1落在射线OB上,点A绕点A1顺时针旋转后的对应点A2落在射线OB上,点A绕点A2顺时针旋转后的对应点A3落在射线OB上,…,连接AA1,AA2,AA3…,依此作法,则∠AAnAn+1等于______度.(用含n的代数式表示,n为正整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
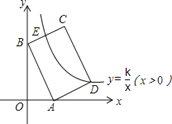
【题目】如图,在平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0),B(0,6)分别在x轴,y轴上,反比例函数y=![]() (x>0)的图象经过点D,且与边BC交于点E,则点E的坐标为__.
(x>0)的图象经过点D,且与边BC交于点E,则点E的坐标为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:圆是最完美的图形,它具有一些特殊的性质:同弧或等弧所对的圆周角相等,一条弧所对的圆周角等于这条弧所对的圆心角的一半……先构造“辅助圆”,再利用圆的性质将问题进行转化,往往能化隐为显、化难为易。
解决问题:如图,点A与点B的坐标分别是(1,0),(5,0),点P是该直角坐标系内的一个动点.
(1)使∠APB=30°的点P有_______个;
(2)若点P在y轴正半轴上,且∠APB=30°,求满足条件的点P的坐标;
(3)设sin∠APB=m,若点P在y轴上移动时, 满足条件的点P有4个,求m的取值范围.
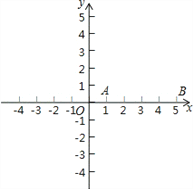
查看答案和解析>>
科目:初中数学 来源: 题型:
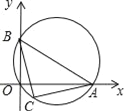
【题目】如图,点A、B分别在x轴、y轴上(OA>OB),以AB为直径的圆经过原点O,C是![]() 的中点,连结AC,BC.下列结论:①AC=BC;②若OA=4,OB=2,则△ABC的面积等于5;③若OA﹣OB=4,则点C的坐标是(2,﹣2).其中正确的结论有( )
的中点,连结AC,BC.下列结论:①AC=BC;②若OA=4,OB=2,则△ABC的面积等于5;③若OA﹣OB=4,则点C的坐标是(2,﹣2).其中正确的结论有( )
A. 3个 B. 2个 C. 1个 D. 0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣4,3),B(﹣3,1),C(﹣1,3).
(1)请按下列要求画图:
①平移△ABC,使点A的对应点A1的坐标为(﹣4,﹣3),请画出平移后的△A1B1C1;
②△A2B2C2与△ABC关于原点O中心对称,画出△A2B2C2.
(2)若将△A1B1C1绕点M旋转可得到△A2B2C2,请直接写出旋转中心M点的坐标 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了锻炼身体,强健体魄,小明和小强约定每天在两家之间往返长跑20分钟. 两家正好在同一直线道路边上,某天小明和小强从各自的家门口同时出发,沿两家之间的直线道路按各自的速度匀速往返跑步,已知小明的速度大于小强的速度. 在跑步的过程中,小明和小强两人之间的距离y(米)与他们出发的时间x(分钟)之间的关系如图所示,在他们3次相遇中,离小明家最近那次相遇时距小明家____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)一个两位数A,十位数字为a,个位数字为b,交换a和b的位置,得到一个新的两位数B,则A+B一定能被______整除,A-B一定能被______整除;
(2)一个三位数M,百位数字为a,十位数字为b,个位数字为c(a,b,c均为1至9的整数),交换a和c的位置,得到一个新的三位数N.请用含a、b、c的式子分别表示数N与M-N;
(3) 若(2)中a比b大1,M比N大792,求M.
查看答案和解析>>
科目:初中数学 来源: 题型:
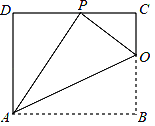
【题目】如图,已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的点P处,折痕与BC交于点O.
(1)求证:△OCP∽△PDA;
(2)若PO:PA=1:2,则边AB的长是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com