
����Ŀ��(1)һ����λ��A,ʮλ����Ϊa,��λ����Ϊb,����a��b��λ��,�õ�һ���µ���λ��B,��A+Bһ���ܱ�______����,A-Bһ���ܱ�______������
(2)һ����λ��M,��λ����Ϊa,ʮλ����Ϊb,��λ����Ϊc��a��b��c��Ϊ1��9��������,����a��c��λ��,�õ�һ���µ���λ��N.���ú�a��b��c��ʽ�ӷֱ��ʾ��N��M-N��
(3) ��(2)��a��b��1,M��N��792����M.
���𰸡���1��11��9����2��N=100c+10b+a��M-N=99a-99c,��3��M=981.
�����������������
(1) ������λ������������������֪��A���Ա�ʾΪ10a+b��B���Ա�ʾΪ10b+a. ������������ʽ�ֱ����A+B��A-B�У����Եõ�A+B��A-B�ı���ʽ. �۲�õ��ı���ʽ��֪��A+B�ı���ʽ�к�������11��A-B�ı���ʽ�к�������9����������ĸ���ѵó���С��Ĵ�.
(2) ��ϵ�(1)С�����λ�������ķ�������ؽ��ۣ�������λ������ʽ����ʽ����д����λ��M��N�ı���ʽ��������Щ����ʽ���ɻ��M-N�ı���ʽ.
(3) ���õ�(2)С��õ���M-N�ı���ʽ����ϱ�С������������Եõ�a-c��ֵ. ��a��c��Ϊ1��9�������������ƶϳ�a��c��ֵ. ������֪������b��ֵ. ���õ�(2)С��õ���M�ı���ʽ���ɵõ���M��ֵ.
���������
(1) �������֪����λ��A���Ա�ʾΪ10a+b����λ��B���Ա�ʾΪ10b+a.
A+B=(10a+b)+(10b+a)=11a+11b=11(a+b).
��Ϊa��b��Ϊ����������a+bΪ����.
��Ϊ![]() ������A+Bһ���ܱ�11����.
������A+Bһ���ܱ�11����.
A-B=(10a+b)-(10b+a)=9a-9b=9(a-b).
��Ϊa��b��Ϊ����������a-bΪ����.
��Ϊ![]() ������A-Bһ���ܱ�9����.
������A-Bһ���ܱ�9����.
�ʱ�С��Ӧ��д��11��9.
(2) ��Ϊ��M�İ�λ����Ϊa��ʮλ����Ϊb����λ����Ϊc��������M���Ա�ʾΪ100a+10b+c����M=100a+10b+c.
��Ϊ��N������M������λ��λ�ϵ����ֵõ��ģ�������N���Ա�ʾΪ100c+10b+a.
�����M-N=(100a+10b+c)-(100c+10b+a)=99a-99c.
����������N=100c+10b+a��M-N=99a-99c.
(3) ��ΪM��N��792��M-N=99a-99c������M-N=99a-99c=99(a-c)=792.
�����a-c=8.
��Ϊa��c��Ϊ1��9��������a-c=8������a=9��c=1.
��Ϊa��b��1������b=a-1=9-1=8.
��Ϊa=9��b=8��c=1������M=100a+10b+c=![]() =981����M=981.
=981����M=981.


 ��ʦ������Ԫ��ĩ���100��ϵ�д�
��ʦ������Ԫ��ĩ���100��ϵ�д� ��У������Ԫͬ��ѵ��������ϵ�д�
��У������Ԫͬ��ѵ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������y2+4y+8����Сֵ�Ľ����̣�
�⣺y2+4y+8=y2+4y+4+4=��y+2��2+4
�ߣ�y+2��2��0
�ࣨy+2��2+4��4
��y2+4y+8����СֵΪ4��
��������Ľ����̣���x2��2x+3����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ε����֮��Ϊ9��16,��С�����ε��ܳ�Ϊ6����,��������ε��ܳ�Ϊ_______����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һԪ���η���x2��10x+21��0������ǡ���ǵ��������εĵױ߳�����������õ��������ε��ܳ�Ϊ��������
A. 13B. 17C. 13��17D. ����ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������У������ж���ABC![]() ��DEF���ǣ� ��
��DEF���ǣ� ��
A. AB=DE,��B=��E����C=��F B. AC=DF,BC=EF,��C=��F
C. AB=FE,��A=��D,��B=��E D. AB=DE,BC=EF,AC=DF
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
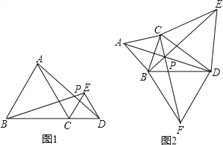
����Ŀ����1����ͼ1����ABC����CDE���ǵȱ������Σ���B��C��D���㹲�ߣ�����AD��BE�ཻ�ڵ�P����֤��BE=AD��
��2����ͼ2������BCD�У���BCD��120�����ֱ���BC��CD��BDΪ������BCD�ⲿ���ȱ�������ABC���ȱ�������CDE�͵ȱ�������BDF������AD��BE��CF���ڵ�P�����н�������ȷ����_________��ֻ����ż��ɣ�
��AD=BE=CF���ڡ�BEC=��ADC���ۡ�DPE=��EPC=��CPA=60����
��3����ͼ2���ڣ�2���������£���֤��PB+PC+PD=BE��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com