
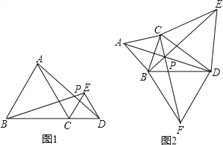
����Ŀ����1����ͼ1����ABC����CDE���ǵȱ������Σ���B��C��D���㹲�ߣ�����AD��BE�ཻ�ڵ�P����֤��BE=AD��
��2����ͼ2������BCD�У���BCD��120�����ֱ���BC��CD��BDΪ������BCD�ⲿ���ȱ�������ABC���ȱ�������CDE�͵ȱ�������BDF������AD��BE��CF���ڵ�P�����н�������ȷ����_________��ֻ����ż��ɣ�
��AD=BE=CF���ڡ�BEC=��ADC���ۡ�DPE=��EPC=��CPA=60����
��3����ͼ2���ڣ�2���������£���֤��PB+PC+PD=BE��
���𰸡���1��BE=AD��2�� �٢ڢ�����ȷ����3��BE=PB+PM+ME=PB+PC+PD��
�������������������1�����ݵȱ������ε����ʵó�BC=AC��CE=CD�� ![]() �����
�����![]() ��֤��
��֤��![]() ���ɣ�
���ɣ�
��2�����BC=AC��CE=CD�� ![]() ��
�� ![]() ��֤
��֤![]() ���Ƴ�
���Ƴ�![]() ��
�� ![]() ��ͬ��
��ͬ��![]() ���Ƴ�BE=CF��
���Ƴ�BE=CF�� ![]() ������
������![]() �Ƴ�
�Ƴ�![]() �����
�����![]() ���������
���������![]() ��ͬ�����
��ͬ�����![]() ��
��
��3����PE�Ͻ�ȡPM=PC������CM�����![]() �����
�����![]() �ǵȱ������Σ��Ƴ�CP=CM��
�ǵȱ������Σ��Ƴ�CP=CM�� ![]() ��֤
��֤![]() ���Ƴ�PD=ME���ɣ�
���Ƴ�PD=ME���ɣ�
���������
��1���ߡ�ABC����CDE���ǵȱ�������
��BC=AC��CE=CD���� ACB=��DCE=60��
���BCE=��ACD
���BCE�ա�ACD��SAS��
��BE=AD
��2���٢ڢ�����ȷ��
��![]() ��
��![]() ���ǵȱ������Σ�
���ǵȱ������Σ�
��![]() ��
�� ![]() ��
�� ![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
![]()
![]()
![]()
![]()
��![]()
��![]() ��
�� ![]() ��
��
�����ȷ��
ͬ��![]()
��BE=CF��
��![]() ��
��
�����ȷ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
ͬ��![]() ��
��![]()
�����ȷ��
�ʴ�Ϊ���٢ڢ���
��3�� ��PE�Ͻ�ȡPM=PC������CM
�ɣ�1����֪����BCE�ա�ACD��SAS��
���1=��2
��CD��BE���ڵ�G������CGE����PGD��
�ߡ�1=��2����CGE=��PGD
���DPG=��EC G=60��ͬ����CPE=60��
���CPM�ǵȱ�������
��CP=CM����PMC=60����
���CPD=��CME="120" ����
�ߡ�1=��2��
���CPD�ա�CME��AAS����
��PD=ME��
��BE=PB+PM+ME=PB+PC+PD��



 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʵ��p��q�� �����÷���min��p�� q����ʾp��q�����н�С��������min ��1��2��=1����min��2x+1�� 1��=x�� ��x=___.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)һ����λ��A,ʮλ����Ϊa,��λ����Ϊb,����a��b��λ��,�õ�һ���µ���λ��B,��A+Bһ���ܱ�______����,A-Bһ���ܱ�______������
(2)һ����λ��M,��λ����Ϊa,ʮλ����Ϊb,��λ����Ϊc��a��b��c��Ϊ1��9��������,����a��c��λ��,�õ�һ���µ���λ��N.���ú�a��b��c��ʽ�ӷֱ��ʾ��N��M-N��
(3) ��(2)��a��b��1,M��N��792����M.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������P��ƽ��ֱ������ϵ�а�ͼ�м�ͷ��ʾ�����˶�����1�δ�ԭ���˶����㣨1��1������2�ν����˶����㣨2��0������3�ν����˶����㣨3��2�����������������˶����ɣ�������2017���˶�����P��������______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����|��a|=a��������a��ȡֵ����ʹ���ʽ�ӳ������ǣ�������
A.0
B.1
C.2
D.aȡ�κθ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������Ʊ�۸����±���ʾ:

ijУ���꼶�ס��������100����ȥ�ù����б�ҵ�����,���мװ���50����,�Ұ��50��,�����Ϊ��λ�ֱ�����Ʊ,������һ��Ӧ��920Ԫ;�������������������Ϊһ�����幺Ʊ,һ��Ҫ��515Ԫ,�ʼס�������ֱ��ж�����?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������3m��������3m����ô��5m��ʾ �� ��
A. ����5m B. ������5m C. ������5m D. ����5m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC������A����B����C�ĶԱ߷ֱ��Ϊ![]() ��
��![]() ��
��![]() �����������������ж���ABCΪֱ�������ε����� ����
�����������������ж���ABCΪֱ�������ε����� ����
A����A+��B=��C
B����A�á�B�á�C =1��2��3
C��![]()
D��![]() ��
��![]() ��
��![]() =3��4��6
=3��4��6
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com