
【题目】已知a、b、c分别为△ABC 的三边长,且![]() ,△ABC是直角三角形吗?为什么?
,△ABC是直角三角形吗?为什么?
【答案】△ABC是直角三角形,理由见解析.
【解析】试题分析:作Rt△A′B′C′,使∠C′=90°,B′C′=BC=a,A′C′=AC=b,由勾股定理求出A′B′=AB,再根据SSS证明△ABC≌△A′B′C′,由全等三角形的对应角相等即可得出∠C=∠C′=90°.
试题解析:证明:作Rt△A′B′C′,使∠C′=90°,B′C′=BC=a,A′C′=AC=b,

由勾股定理,得A′B′2=B′C′2+A′C′2=a2+b2,
∵a2+b2=c2,AB=c,
∴A′B′2=AB2,
∴A′B′=AB.
在△ABC与△A′B′C′中,
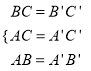 ,
,
∴△ABC≌△A′B′C′(SSS),
∴∠C=∠C′=90°,
即△ABC是直角三角形。


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】解答下列各题:
(1)(﹣3.6)+(+2.5)
(2)-![]() ﹣(﹣3
﹣(﹣3![]() )﹣2
)﹣2![]() +
+![]()
(3)(﹣49)﹣(+91)﹣(﹣5)+(﹣9)
(4)﹣5﹣(﹣11)+2![]() ﹣(﹣
﹣(﹣![]() )
)
(5)3![]() ﹣(﹣
﹣(﹣![]() )+2
)+2![]() +(﹣
+(﹣![]() )
)
(6)![]() ﹣|﹣1
﹣|﹣1![]() |﹣(+2
|﹣(+2![]() )﹣(﹣2.75)
)﹣(﹣2.75)
(7)(﹣7)﹣(﹣11)+(﹣9)﹣(+2)
(8)(﹣4![]() )﹣(+5
)﹣(+5![]() )﹣(﹣4
)﹣(﹣4![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中,不能判断△ABC![]() △DEF的是( )
△DEF的是( )
A. AB=DE,∠B=∠E,∠C=∠F B. AC=DF,BC=EF,∠C=∠F
C. AB=FE,∠A=∠D,∠B=∠E D. AB=DE,BC=EF,AC=DF
查看答案和解析>>
科目:初中数学 来源: 题型:
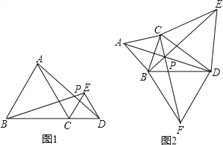
【题目】(1)如图1,△ABC和△CDE都是等边三角形,且B、C、D三点共线,联结AD、BE相交于点P,求证:BE=AD;
(2)如图2,在△BCD中,∠BCD<120°,分别以BC、CD和BD为边在△BCD外部作等边三角形ABC、等边三角形CDE和等边三角形BDF,联结AD、BE和CF交于点P,下列结论中正确的是_________(只填序号即可)
①AD=BE=CF;②∠BEC=∠ADC;③∠DPE=∠EPC=∠CPA=60°;
(3)如图2,在(2)的条件下,求证:PB+PC+PD=BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】检修小组从A地出发,在东西路上检修线路,若规定向东行驶的路程为正数,向西行驶的路程为负数,一天中行驶记录(单位;千米)如下: ![]()
(1)收工时检修小组在A地的哪侧,距A地多远?
(2)若每千米耗油0.3升,从出发到收工共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有25名同学参加某项比赛,预赛成绩各不相同,取前13名参加决赛,其中一名同学已经知道自己的成绩,能否进入决赛,只需要再知道这25名同学成绩的( )
A.最高分
B.中位数
C.方差
D.平均数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com