
【题目】△ABC中,∠A,∠B,∠C的对边分别记为![]() ,
,![]() ,
,![]() ,由下列条件不能判定△ABC为直角三角形的是( ).
,由下列条件不能判定△ABC为直角三角形的是( ).
A.∠A+∠B=∠C
B.∠A∶∠B∶∠C =1∶2∶3
C.![]()
D.![]() ∶
∶![]() ∶
∶![]() =3∶4∶6
=3∶4∶6
【答案】D.
【解析】
试题分析:A选项能判定△ABC为直角三角形,因为三角形的内角和是180度,所以∠A+∠B+∠C=180°,当∠A+∠B=∠C 时 ,此式转换成∠C+∠C=180°,2∠C=180°,∠C=90°,所以可判定△ABC为直角三角形,B选项能判定△ABC为直角三角形,因为三角形的内角和是180度,所以∠A+∠B+∠C=180°,当∠A∶∠B∶∠C =1∶2∶3时,最大角∠C=180°×![]() =90°,所以可判定△ABC为直角三角形;C选项能判定△ABC为直角三角形,根据勾股定理的逆定理,如果三角形的两条边的平方和等于第三边的平方,那么这个三角形就是直角三角形,当
=90°,所以可判定△ABC为直角三角形;C选项能判定△ABC为直角三角形,根据勾股定理的逆定理,如果三角形的两条边的平方和等于第三边的平方,那么这个三角形就是直角三角形,当![]() 时,移项得:
时,移项得:![]() ,所以也可判定△ABC为直角三角形;D选项不能判定△ABC为直角三角形,因为当
,所以也可判定△ABC为直角三角形;D选项不能判定△ABC为直角三角形,因为当![]() ∶
∶![]() ∶
∶![]() =3∶4∶6时,设这三边为3x,4x,6x,因为(3x)2+(4x)2≠(6x)2,根据勾股定理的逆定理,△ABC不是直角三角形;综上所述,本题选D.
=3∶4∶6时,设这三边为3x,4x,6x,因为(3x)2+(4x)2≠(6x)2,根据勾股定理的逆定理,△ABC不是直角三角形;综上所述,本题选D.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
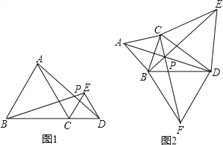
【题目】(1)如图1,△ABC和△CDE都是等边三角形,且B、C、D三点共线,联结AD、BE相交于点P,求证:BE=AD;
(2)如图2,在△BCD中,∠BCD<120°,分别以BC、CD和BD为边在△BCD外部作等边三角形ABC、等边三角形CDE和等边三角形BDF,联结AD、BE和CF交于点P,下列结论中正确的是_________(只填序号即可)
①AD=BE=CF;②∠BEC=∠ADC;③∠DPE=∠EPC=∠CPA=60°;
(3)如图2,在(2)的条件下,求证:PB+PC+PD=BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有25名同学参加某项比赛,预赛成绩各不相同,取前13名参加决赛,其中一名同学已经知道自己的成绩,能否进入决赛,只需要再知道这25名同学成绩的( )
A.最高分
B.中位数
C.方差
D.平均数
查看答案和解析>>
科目:初中数学 来源: 题型:
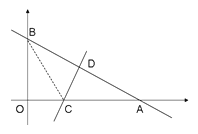
【题目】如图:一次函数y=-![]() x+6的图象与x轴和y轴分别交于点A和B ,再将△ AOB沿直线CD对折,使点A与点B重合。直线CD与x轴交于点C,与AB交于点D.
x+6的图象与x轴和y轴分别交于点A和B ,再将△ AOB沿直线CD对折,使点A与点B重合。直线CD与x轴交于点C,与AB交于点D.
(1)点A的坐标为 ,点B的坐标为 。
(2)求OC的长度 ;
(3)在x轴上有一点P,且△PAB是等腰三角形,不需计算过程,直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com