
【题目】若a、b互为相反数,b、c互为倒数,并且m的立方等于它本身。
(1)求![]() +ac值.
+ac值.
(2)若a>1,且m<0,S=|2a-3b|-2|b-m|-|b+![]() |,求2a-S的值.
|,求2a-S的值.
(3)若m≠0,试讨论:x为有理数时|x+m|-|x-m|是否存在最大值?若存在求出这个最大值;若不存在,请说明理由.
【答案】(1)-1;(2)-![]() ;(3)存在最大值,最大值为2.
;(3)存在最大值,最大值为2.
【解析】
(1)先根据a、b互为相反数,b、c互为倒数,得出a+b=0,bc=1,再代入所求代数式进行计算;
(2)根据a>1及m的立方等于它本身,把S进行化简,再代入所求代数式进行计算;
(3)根据若m≠0,可知m=±1,①当m=1时,代入|x+m|-|x-m|,再根据绝对值的性质去掉绝对值符号,求出代数式的值,
②同理,当m=-1时代入所求代数式,再根据绝对值的性质去掉绝对值符号,求出代数式的值,即可.
解:(1)∵a、b互为相反数,b、c互为倒数,
∴a+b=0,bc=1,
∴ac=-1
∴![]()
(2)∵a>1,
∴b<-1,2a-3b>0,b+![]() <0
<0
∵m的立方等于它本身,且m<0
∴m=-1,b-m=b+1<0
∴s=2a-3b+2b+2+b+![]() =2a+
=2a+![]()
∴2a-s=-![]()
(3)若m≠0,此时m=±1
①若m=1,则|x+m|-|x-m|=|x+1|-|x-1|
当x≤-1时
|x+1|-|x-1|=-x-1+x-1=-2
当-1<x≤1时
|x+1|-|x-1|=x+1+x-1=2x
当x>1时
|x+1|-|x-1|=x+1-x+1=2
∴当x为有理数时,存在最大值为2;
②若m=-1
同理可得:当x为有理数时,存在最大值为2.
综上所述,当m=±1,x为有理数时,|x+m|-|x-m|存在最大值为2.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,过点A引射线AH,交边CD于点H(点H与点D不重合),通过翻折,使点B落在射线AH上的点G处,折痕AE交BC于点E,延长EG 交CD于点F.如图①,当点H与点C重合时,易证得FG=FD(不要求证明);如图②,当点H为边CD上任意一点时,求证:FG=FD.
【应用】在图②中,已知AB=5,BE=3,则FD= ,△EFC的面积为 .(直接写结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:(1) ∠DCF=![]() ∠BCD;(2)EF=CF;(3)S△CDF=S△CEF;(4)∠DFE=3∠AEF.其中正确结论的个数是( )
∠BCD;(2)EF=CF;(3)S△CDF=S△CEF;(4)∠DFE=3∠AEF.其中正确结论的个数是( )
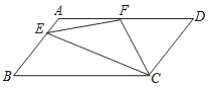
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲船逆水,静水速度为28海里/时;乙船顺水,静水速度为12海里/时,两船相距60海里.已知水流速度为3海里/时,两船同时相向而行.
(1)两船同时航行1小时,求此时两船之间的距离;
(2)再(1)的情况下,两船再继续航行1小时,求此时两船之间的距离;
(3)求两船从开始航行到两船相距12海里,需要多长时间?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快递员小王下午骑摩托车从总部出发,在一条东西走向的街道上来回收送包裹.他行驶的情况记录如下(向东记为“![]() ”,向西记为“
”,向西记为“![]() ”,单位:千米):
”,单位:千米):
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)小王最后是否回到了总部?
(2)小王离总部最远是多少米?在总部的什么方向?
(3)如果小王每走![]() 米耗油
米耗油![]() 毫升,那么小王下午骑摩托车一共耗油多少毫升?
毫升,那么小王下午骑摩托车一共耗油多少毫升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蜗牛从某点O开始沿东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬行的各段路程依次为(单位:厘米):![]() .问:
.问:
(1)蜗牛最后是否回到出发点O?
(2)蜗牛离开出发点O最远是多少厘米?
(3)在爬行过程中,如果每爬行1厘米奖励一粒芝麻,则蜗牛可得到多少粒芝麻?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习过绝对值之后,我们知道:|5-2|表示 5 与 2 的差的绝对值,实际上也可理解为 5 与 2 两数在数轴上所对应的两点之间的距离:|5+2|表示 5 与-2 的差的绝对值,实际上也可理解为 5 与-2 两数在数轴上所对应的两点之间的距离. 试探究解决以下问题:
⑴|x+6|可以理解为 与 两数在数轴上所对应的两点之间的距离;
⑵找出所有符合条件的整数 x,使|x+1|+|x-2|=3 成立;
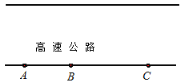
⑶如图,在一条笔直的高速公路旁边依次有 A、B、C 三个城市,它们距高速公路起点的距离分别是 567km、689km、889km.现在需要在该公路旁建一个物流集散中心 P,请直接指出该物流集散中心 P 应该建设在何处,才能使得 P 到三个城市的距离之和最小?这个最小距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】701班小强买了张100元的深圳通乘车卡,如果他乘车的次数用![]() 表示,则记录他每次乘车后的余额n (元)如下表:
表示,则记录他每次乘车后的余额n (元)如下表:
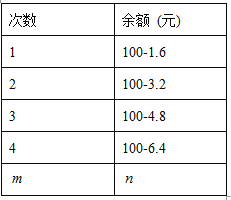
(1)写出余额n与乘车的次数m的关系式.
(2)利用上述关系式计算小强乘了23次车还剩下多少元?
(3)小强最多能乘几次车?
查看答案和解析>>
科目:初中数学 来源: 题型:
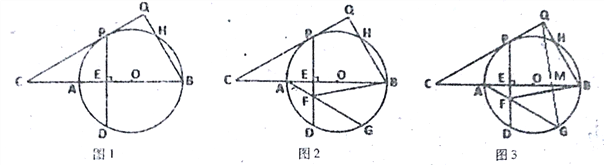
【题目】已知:如图,AB为⊙O的直径,C是BA延长线上一点,CP切⊙O于P,弦PD⊥AB于E,过点B作BQ⊥CP于Q,交⊙O于H.
(1)如图1,求证:PQ=PE;
(2)如图2,G是圆上一点,∠GAB=30![]() ,连接AG交PD于F,连接BF,tan∠BFE=
,连接AG交PD于F,连接BF,tan∠BFE=![]() ,求∠C的度数;
,求∠C的度数;
(3)如图3,在(2)的条件下,PD=6![]() ,连接QG交BC于点M,求QM的长.
,连接QG交BC于点M,求QM的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com