
【题目】如图,点E在菱形ABCD的对角线BD上,连接AE,且AE=BE,⊙O是△ABE的外接圆,连接OB.
(1)求证:OB⊥BC;
(2)若BD=![]() ,tan∠OBD=2,求⊙O的半径.
,tan∠OBD=2,求⊙O的半径.
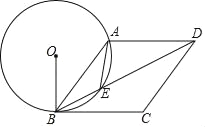
【答案】(1)见解析;(2)5
【解析】整体分析:
(1)连接OA、OE,设OE交AB于F,须证∠OBE+∠CBD=90°,由于∠CBD=∠ABD,∠OBE=∠OEB,即要证∠BEF+∠EBF=90°,由垂径定理可得OE⊥AB;(2)连接AC交BD于G,证得∠GCB=∠OBD,求出BC,CG,在Rt△BEF中,求EF,在Rt△OBF中,用勾股定理列方程求半径.
(1)证明:连接OA、OE,设OE交AB于F,
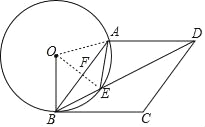
∵AE=BE,∴∠AOE=∠BOE,
∵OA=OB,∴AF=BF,OE⊥AB,
∴∠OFB=∠BFE=90°,∴∠BEF+∠EBF=90°,
∵四边形ABCD是菱形,∴∠CBD=∠ABD,
∵OB=OE,∴∠OBE=∠OEB,
∴∠OBE+∠CBD=90°,∴∠OBC=90°,
∴OB⊥BC;
(2)解:连接AC交BD于G,
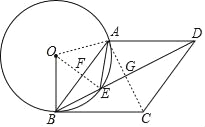
∵四边形ABCD是菱形,∴AB=BC,AC⊥BD,BG=![]() BD=
BD=![]() ,
,
∴∠BGC=90°,∴∠GCB+∠GBC=90°,
∵∠OBD+∠CBG=90°,∴∠GCB=∠OBD,
在Rt△BCG中,tan∠GCB=tan∠OBD=2,
∴![]() =2,∴CG=
=2,∴CG=![]() ,
,
∴BC=![]() =
=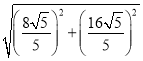 =8,
=8,
∴AB=8,∴BF=4,
在Rt△BEF中,tan∠BEF=tan∠OBD=2,
∴![]() =2,∴EF=2,
=2,∴EF=2,
设⊙O的半径为r,
在Rt△BOF中,OF2+BF2=OB2,
(r﹣2)2+42=r2,解得:r=5,
即⊙O的半径为5.


科目:初中数学 来源: 题型:
【题目】已知:M=3a2+4ab -5a-6,N=a2-2ab-4
(1)化简:5M-(3N + 4M),结果用含a、b的式子表示.
(2)若式子5M-(3N + 4M)的值与字母a的取值无关,求b4+![]() M-
M-![]() N-
N-![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快递员小王下午骑摩托车从总部出发,在一条东西走向的街道上来回收送包裹.他行驶的情况记录如下(向东记为“![]() ”,向西记为“
”,向西记为“![]() ”,单位:千米):
”,单位:千米):
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)小王最后是否回到了总部?
(2)小王离总部最远是多少米?在总部的什么方向?
(3)如果小王每走![]() 米耗油
米耗油![]() 毫升,那么小王下午骑摩托车一共耗油多少毫升?
毫升,那么小王下午骑摩托车一共耗油多少毫升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习过绝对值之后,我们知道:|5-2|表示 5 与 2 的差的绝对值,实际上也可理解为 5 与 2 两数在数轴上所对应的两点之间的距离:|5+2|表示 5 与-2 的差的绝对值,实际上也可理解为 5 与-2 两数在数轴上所对应的两点之间的距离. 试探究解决以下问题:
⑴|x+6|可以理解为 与 两数在数轴上所对应的两点之间的距离;
⑵找出所有符合条件的整数 x,使|x+1|+|x-2|=3 成立;
⑶如图,在一条笔直的高速公路旁边依次有 A、B、C 三个城市,它们距高速公路起点的距离分别是 567km、689km、889km.现在需要在该公路旁建一个物流集散中心 P,请直接指出该物流集散中心 P 应该建设在何处,才能使得 P 到三个城市的距离之和最小?这个最小距离是多少?
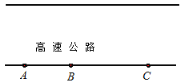
查看答案和解析>>
科目:初中数学 来源: 题型:
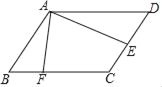
【题目】如图,在![]() ABCD中,点E为CD的中点,点F在BC上,且CF=2BF,连接AE,AF,若AF=
ABCD中,点E为CD的中点,点F在BC上,且CF=2BF,连接AE,AF,若AF=![]() ,AE=7,tan∠EAF=
,AE=7,tan∠EAF=![]() ,则线段BF的长为__________.
,则线段BF的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】701班小强买了张100元的深圳通乘车卡,如果他乘车的次数用![]() 表示,则记录他每次乘车后的余额n (元)如下表:
表示,则记录他每次乘车后的余额n (元)如下表:
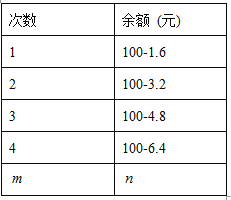
(1)写出余额n与乘车的次数m的关系式.
(2)利用上述关系式计算小强乘了23次车还剩下多少元?
(3)小强最多能乘几次车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,BC=8,P,Q分别是直线BC,AB上的两个动点,AE=2,△AEQ沿EQ翻折形成△FEQ,连接PF,PD,则PF+PD的最小值是().
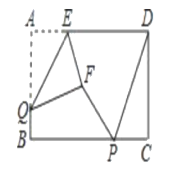
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举行“传承好家风”征文比赛,已知每篇参赛征文成绩记m分(60≤m≤100),组委会从1000篇征文中随机抽取了部分参赛征文,统计了他们的成绩,并绘制了如下不完整的两幅统计图表.

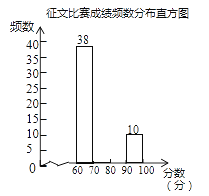
请根据以上信息,解决下列问题:
(1)征文比赛成绩频数分布表中c的值是________;
(2)补全征文比赛成绩频数分布直方图;
(3)若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“幸福是奋斗出来的”,在数轴上,若C到A的距离刚好是3,则C点叫做A的“幸福点”,若C到A、B的距离之和为6,则C叫做A、B的“幸福中心”
(1)如图1,点A表示的数为﹣1,则A的幸福点C所表示的数应该是 ;
(2)如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为﹣2,点C就是M、N的幸福中心,则C所表示的数可以是 (填一个即可);
(3)如图3,A、B、P为数轴上三点,点A所表示的数为﹣1,点B所表示的数为4,点P所表示的数为8,现有一只电子蚂蚁从点P出发,以2个单位每秒的速度向左运动,当经过多少秒时,电子蚂蚁是A和B的幸福中心?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com